SHEMETOV YEVGENY. STUDIES OF PHASE TRANSITIONS IN THE UNITED A2BX4 STRUCTURE β-K2SO4 METHOD NUCLEAR QUADRUPOLE RESONANCE
English abstract § 1.1 § 1.2 §1.3 § 1.4 § 2.1 § 2.2 §2.3 §2.4 § 3.1 § 3.2 § 3.3 § 3.4 § 4.1 § 4.2 § 4.3 § 4.4 Reference Template pdf abstract
§ 4.4 Discussion of the phase diagrams in the framework of theoretical models "devil's staircase".
In conclusion, we provide a synthesis of the experimental P-T diagram of Rb2ZnBr4 according NQR (Fig.4.35) and compare it with the theoretical phase diagrams obtained by numerical methods. Calculations performed in [15,12,121] are based on the anisotropic Ising model with the interaction up to three neighbors. We are interested in that part of the phase diagram, where realized structure with a period close to 1/3 and 1/4 Fig.4.38a. In this diagram, the value of qδ = l/3 corresponds to the configuration of spins <12> (one up, two down), qδ = 1/4- <121>, qδ = 5/17- <1121212 (12) 2>; qδ =3/10-<112(12) 2>; qδ = 3/10- <112 (12) 2>; etc. If this diagram spend dashed line, as shown on Fig.4.38a, and relate it to the experimental scale temperature at atmospheric pressure, is located above this line, the phase diagram [121], would be enough comparable to the experimental P-T diagram obtained world. In this case the transition to the modification of this model in the framework of the pseudo-spin variables [12], the region of existence of structures with different configurations can be changed (Fig.4.38b).
A somewhat different approach developed in recent years [12]. Its foundations were laid by a modification of the parabolic model of Frenkel-Cantor and put nesimorfny symmetry element, which acts as a nonlinear part of the polarization of communication between sublattices. With the increase of the contribution of the nonlinear polarization PNL , in a structure with symmetry series Pnma, phase fractions of 1/3 and 1/4 respectively decrease and increase, appear between lower-order symmetry structures (Fig.4.39). Inset on a larger part of the diagram shows Fig.4.39 Aubrey, which can be compared with our P-T phase diagram.
When considering the field of existence of the phase 2/7, located between phases 1/3", 1/4" phase diagram Aubrey and lines separating phases 1/3", 1/3 and 5/17, we can imagine that in our case there a fine structure of these regions (as shown in
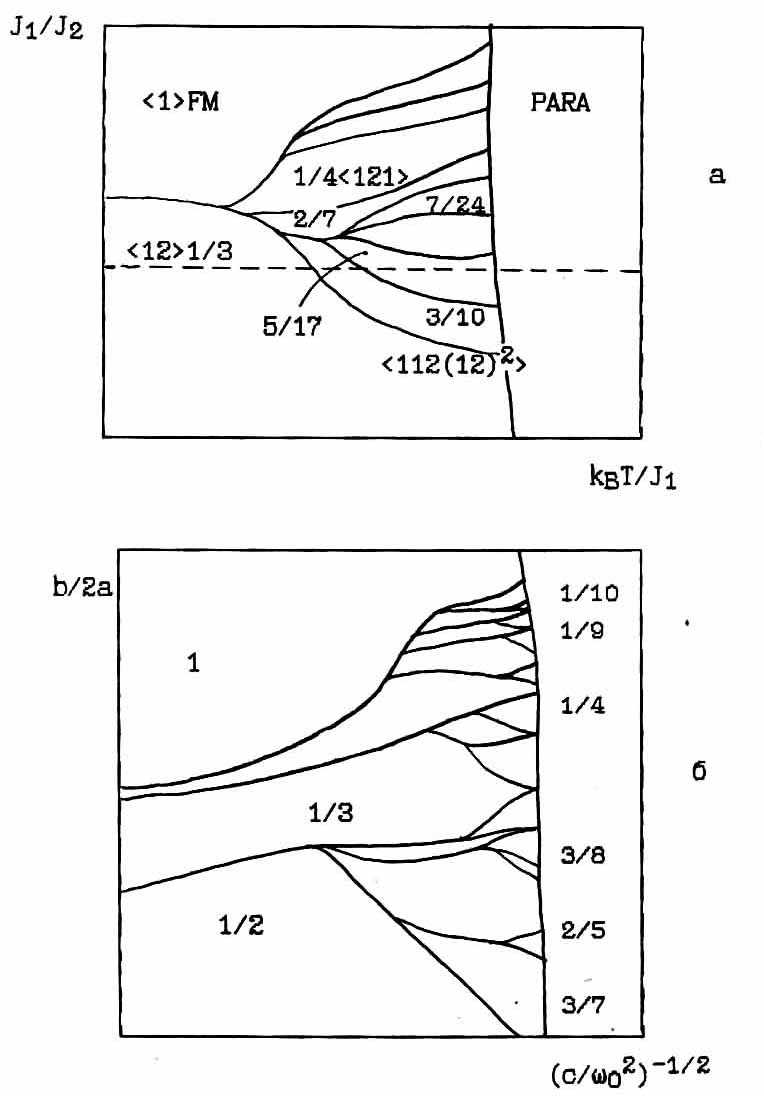
Fig.4.38.
a) theoretical diagram Celka [121];
b) phase diagram Aubrey [5].
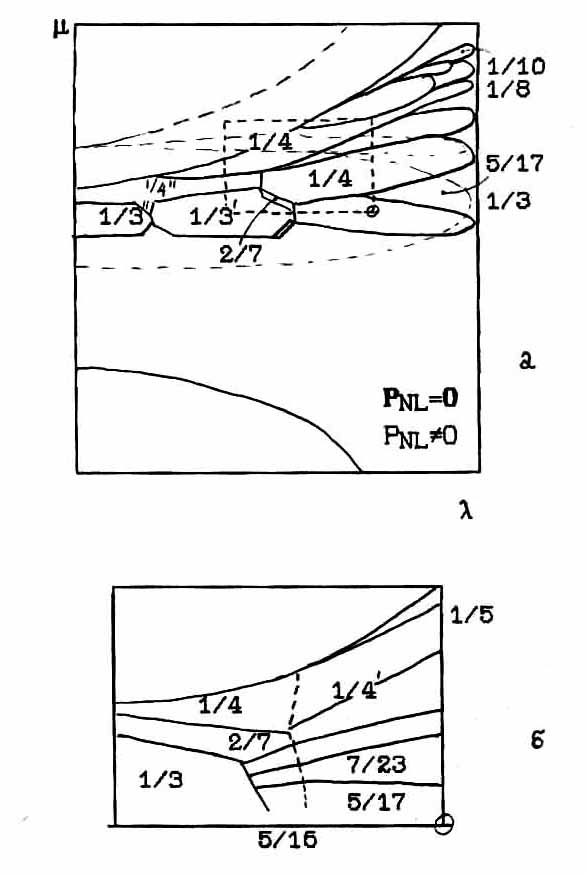
Fig.4.39. Theoretical phase diagram of the polarization model Aubry [12].
Fig.4.39b as intermediate steps between 1/3 and 5/17, and between 5/17 and 2/7. In this case, the phase diagram obtained RZB NQR based on the values of the wave vectors of the measured diffraction neutron diffraction well compared with the theoretical phase diagram in the model Aubrey [12].
As follows from numerous data on the experimental study of the phase diagrams of various systems with frustrating interactions diagrams complication occurs not only in the case of registration of more distant neighbors across the anisotropy axis of the system, but with the introduction of structural disorder (random field). The latter may be due to impurities, H2 bonds, nuclear isotopes, as well as presence in the crystal layers or surface phases of another structure. Omitting, however, the discussion neutron diffraction [124, 21] and scaling [123] type of behavior that can be observed in this case, we dwell on the reasons leading to the stochastic regime celebrated applications of three-dimensional and two-ANNNI models [13]. If, for example, the energy of the system is close to the case of a tripling of the unit cell (or j ≈π/3), the average structure is a topological articulation sоlitons, antisolitons and their random combination. Depending on the interaction, some combinations will be energetically more favorable. Such chaotic phase will be metastable, and the degree of metastability depends on the communication parameter disproportion to the elastic energy. Infinite (or finite) number of stable states of a set of "devil staircase" can be separated by energy barriers and the real system can not relax to the ground state in a finite time.
In this mode, there are two cases: weak and strong interaction potential [13,120]. In this case, when the distance between solitons small incommensurate phase is stable. When the distance between the solitons, repulsive interaction between them can not overcome the pinning lattice and observed soft chaotic regime. With significant excess disproportionate period compared with the lattice period, high-temperature phase is stabilized. Here it is possible to conduct a similar cluster pretransition ordering.
At strengthening ties between the sublattices ANNNI model (strong potential), the width of the chaotic regime can greatly increase and the incommensurate phase will be able to include some long-period phases. For example, instead of the phase q = 2p/4*(l-qd) in the range of wave vector q ± Dq four possible modulation states q =3/16 = 1/4*(1-1/4). The phases will differ phase shift value j= j0 ± Dj close to p/4. When these four long-period would be two chaotic phase. When reducing the magnitude of the wave vector number energetically close phase will increase. Each incommensurate phase is represented by a set of long-period and chaotic phases. In this case, should be observed smoothed (incomplete) mode ↔Devil's starcase», as opposed to purely chaotic regime, where the wave vector varies according to the classical (smooth) mode Devil's starcase'. In this case (for large values of the period disparity) is true incommensurate phase is not realized.
To analyze this possibility in our case, we, on the [120], should appeal to the structure of Pnma. As is known, the structure of A2BX4 type β-K2SO4 in a certain layer ab-plane of the two centers of gravity двухBX4 tetrahedra are located at the same level as the ion A (Fig.3.14). Between coats z = l/4 and z = 3/4 A ions are remaining. When considering the structure within a single layer, it can be assumed that the electrostatic force acting within the layer is not stable, whereby there is the rotational mode, which each tetrahedron rotates so that the other two in this tetrahedron unit cell are rotated in opposite directions. Structure should stabilize spatial redistribution of the charge between the ion A and one of the X atoms of the tetrahedron. Potential energy within the layer can be represented by a double pit: a polynomial of fourth degree of j. Interaction between the layers appear in the repulsion between the top and the base of the tetrahedron tetrahedron lying in another layer, and through A ions. When along the c direction has two layers on the lattice constant (such as in Rb2ZnBr4), the potential energy of interaction of ions can be characterized by the rotation of the pyramid in the n-th layer at an angle φjn and is represented in form similar to φ4 discrete tasks ANNNI model [120]:
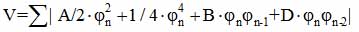
As is known, in this case there are non-linear solutions (Eg "solitons"). For the calculation of the parameters A, B and D need to know the specifics of the interatomic interactions and the structure of the chemical bond. However, some solutions φ4 models have a chaotic regime. As shown in [120,122], in particular cases, for small values of width 1 "solitons" relative lattice constant (narrow solitons), there are several states with high-order proportionality little distance between solitons lo. With an increase lo and reaching its value a certain critical value lcr , a mixed state becomes chaotic behavior with randomly pinned (anti) solitons.
Trying to satisfy neutron diffraction data, X-ray scattering data and RF, we can represent the structure of the incommensurate phase of an infinite set of fragments with a long period, which differ in the non-equivalence of the chemical bond in subfragment located in the structural cell in a certain way. For example, assuming that N4 phase, Rb2ZnBr4 crystal cell 14 has a size of the lattice constant, the substructure it can be composed of two fragments with a length 3a0 and 4a0 of the two in the lattice constants relative to each other spaced randomly (mixed nonlinear solutions). In the primitive description limited fourteen tetrahedra (in their double-well Librational position), we can make a subcell 3a0, for example, one of the tetrahedron in the left and two in the right position, and 4a0 subcell of the two left and two right successive tetrahedra. Then cell 14a0 can be represented on five ways (basic solutions) consistent position two nested cells 3a0 and 4a0 two cells. One of these methods may be more favorable. In the full sense of the overall structure is determined by the specific nonlinear solution.
Spreading such structuring on the high temperature region of Rb2ZnBr4, one can try to describe the transition structure of the 5/17 to 1/3 or 1/4 for each halogen atom tetrahedron through a small redistribution of electron density in a group of neighboring atoms (flash polarization). In implementing such a process cell size is reduced through a series of steps to 3a0 or 4a0. Modulation does not seem continuous displacement of nucleus from state to state, and the redistribution of the electron density of the two ranked energetically close structures 3a0 and 4a0.
According to this concept, according to NQR Rb2ZnBr4 under pressure in a wide temperature range from Ti to 230K near atmospheric pressure observed mixed mode and a long-chaotic behavior. This is evident from a comparison of the observed shape of the spectrum, which is directly after annealing presented blurred frequency distributions. In this case, the diffraction data, where there is a blurred satellite in the same position (≈5/17), see only the periodicity of the structure. At Tc phase transition to a long-F behavior prevails over chaotic (complete). And with increasing pressure to phase H, the chaotic behavior is almost completely disappears and "satanic staircase" seen more clearly (complete). In this phase 2/7 structure is dependent on the prehistory combination phases ≈1/3 and" ≈1/4. N-phase is a mixture of long-period phase with a small admixture of chaotic. As the pressure increases in JC and M phases, the number of energetically equivalent sets of long-period and chaotic phases, according to [13], may increase. The phase transition in this case represent the areas where change is carried out medium wave vector. We can assume that the phase transition M1↔M2 is a change of the wave vector qS chaotic structure of 1/4 to 1/5 or 1/6 through the intermediate value type qS ≈ 0.222 ≈1/4-d. Therefore, diffraction techniques can be observed here another narrow phase, as predicted by the model Aubrey [12] and have been reported in (NH4)2ZnCl4 [47,50] and (NH4)2ZnBr4 (Figure 1.6).
Shape of the resonance lines in the incommensurate phase may reflect a certain type of mixed between states qδ ≈l/4 and qδ ≈l/3 of the nonlinear solutions.
Thus, the comparison of the theoretical phase diagrams with P-T diagram of the NQR data and taking into account the data neutron diffraction scattering, suggesting that an increase in pressure in the RZB should be observed structure type 1/5, 1/6, 1/8 and etc., approaching the Lifshitz point. As for structural changes in phase modulated, one can assume the presence of a substantial Rb2ZnBr4 interactions frustrating crystal spatial symmetry. Framework for describing transformation of the structure and evolution of the NQR spectra, from this point of view, should be sought in the implementation of competition electrical interaction between the sublattices of the structure and its connection with the phonon spectrum. Availability the nonlinear polarization in this class of compounds has long been established. It is due to significant distortion and rotation groups BX4 and inhomogeneous polarization of the electrons in the atomic core In this connection there are substantial electric dipole moments of atomic groups, the values of which differ for each group in both magnitude and direction. Accounting for such a spatially inhomogeneous nonlinear electrical deposits can significantly change the way in the shape description resonance spectra in the compounds of the family A2BX4. Cause of heterogeneity to be found in the intricacies of the nature of the chemical bond.
Finally, we can also make a comparison of theoretical phase diagram Aubrey with experimental data on change in the magnitude of the wave vector qδ in other compounds A2BX4 (Table 4.1).
From the point of view of crystal chemistry, the relative magnitude of the radius of the cation A compound A2BX4 can be divided into two groups. In the first group, with a large cation Cs, the following sequence transforming structures:
.
. In Cs2CdJ4, Cs2CdBr4 sequence transformation structures and size qδ in Jc close to those for Cs2CdJ4. . In the second group, with medium and small radius of the cation, there is a different sequence of transformations of the structure, characterized by low-temperature phase with the space group Pn21 a, but with different multiplicity of the unit cell volume relatively high. So for Rb2ZnBr4 under pressure, we have:
4.1. Table 4.1. Modulation Character and evolution of the family structure in crystals A2BX4 -type structure β-K2SO4
-159 -
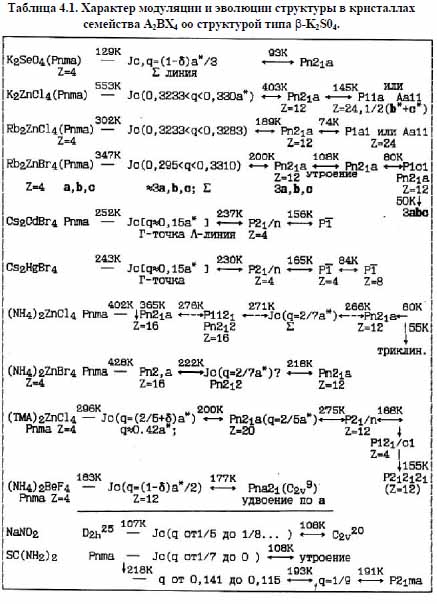

From a comparison of the amount of change of the wave vector qδ within the incommensurate phase at atmospheric pressure (Table 4.1) compounds A2BX4 and taking into account the data for Cs2CdJ4, Cs2ZnJ4 and Rb2ZnBr4 under pressure, we can put isobaric line atmospheric temperature change of each compound from Table. 4.1 .4.1 the theoretical phase diagram and Aubrey Buck. (.4.40), 2 4 , q d , - [12], , . As a result, we obtain the circuit (Fig.4.40), where through the line marked by the particular compound A2BX4 are isobaric atmospheric line qδ experimental measurements in this compound, and the oval area outlined by dashed lines represent stylized model Aubrey polyhedra [12], where the period of the structure does not change, but changes the phase shift between the sublattices model.
.4.40. As can be seen from the presented scheme, despite unconfirmed some experimental data or their limitations, there is sufficient correlation between the known experimental P-T phase diagrams of the generalized phase diagram of Scheme Fig.4.40. Please keep in mind that the cesium compound was isolated as a subclass, characterized by a specific sequence of symmetry transformations associated with the softening of the phonon spectrum near the T point of the Brillouin zone, and the rest - in the subclass - along S line.
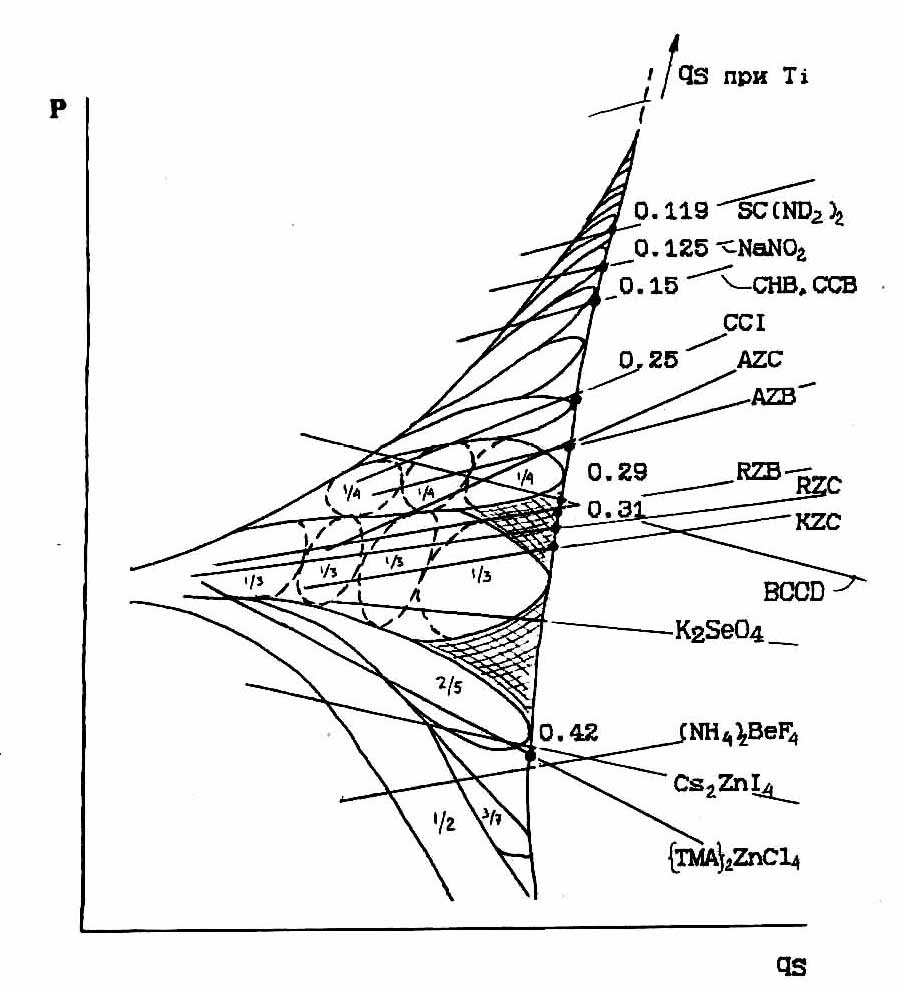
Fig.4.40. Comparison of experimental data on the change of the wave vector qd in various compounds such β-K2SO4 with the theoretical phase diagram [12].
The main of results .
1. NQR for precision studies of phase transitions created Gradientless thermal consoles and high-pressure chamber having an optimal agreement with the receiving part of the standard quadrupole resonance spectrometer.
2. Studied the sequence of phase transitions in Cs2CdJ4. First detected NQR incommensurate phase in this crystal modification β. Complementary experimental methods built circuit symmetry changes. X-ray diffraction analysis confirmed the presence of the incommensurate phase.
3. The sequence of phase transitions in the crystal Cs2ZnJ4 . NQR 127J registered incommensurate phase, found a wide temperature range subtransient ordering. The assumption is made and confirmed the change of symmetry in phase transitions in this compound.
4. The author synthesized and studied by NQR compound (NH4)2ZnJ4. According to transition 1/2↔3/2 127J found three phase transitions. The line shape and features of the temperature dependence of the frequencies suggest that the intermediate phase in the crystal of NH4)2ZnJ4 are disproportionate.
5. Held temperature measuring the TQ1 and Tq2 nuclear spin relaxation 127J. A substantial effect of the spin-spin relaxation of halogen correctness registration form of the resonance line in the incommensurate phase. Two-scale fixed nature of the nuclear dynamics in Cs2ZnJ4.
6. Polymorphic modifications crystal Rb2ZnBr4 and Cs2CdJ4 α↔β - . Found that β -modification in compounds Cs2CdJ4 and Rb2ZnBr4 is metastable. The conditions for the implementation of transition.
7. NQR constructed and investigated P-T phase diagram of Rb2ZnBr4 in the incommensurate phase to pressures greater than 1.0GPa. Detected sequence highly symmetric and disproportionate disordered high-pressure phases. Interpretation of experimental data NQR in the "devil's staircase" is not contrary to the diffraction measurements and theoretical models pseudospin-ANNNI incommensurate phases.
Conclusion
The investigations demonstrate the pulse NQR method in studying disordered structures, including at high hydrostatic pressure.
On the basis of the developed equipment for temperature and high-pressure measurements investigated the sequence of phase transitions in a number of compounds with incommensurate phases.
On the basis of data on the degree of structural ordering and dynamic nucleus used compounds studied can be developed transformation model of atomic structure.
The author is grateful supervisor candidate physical and mathematical sciences A.K. Moskalev for help with the manuscript and helpful suggestions. Thanks Soros Foundation for financial support.
English abstract § 1.1 § 1.2 §1.3 § 1.4 § 2.1 § 2.2 §2.3 §2.4 § 3.1 § 3.2 § 3.3 § 3.4 § 4.1 § 4.2 § 4.3 § 4.4 Reference Template pdf abstract