SHEMETOV YEVGENY. STUDIES OF PHASE TRANSITIONS IN THE UNITED A2BX4 STRUCTURE β-K2SO4 METHOD NUCLEAR QUADRUPOLE RESONANCE
English abstract § 1.1 § 1.2 §1.3 § 1.4 § 2.1 § 2.2 §2.3 §2.4 § 3.1 § 3.2 § 3.3 § 3.4 § 4.1 § 4.2 § 4.3 § 4.4 Reference Template pdf abstract
CONTENTS
|
Introduction . |
page 3 |
|
Chapter 1. Incommensurate modulated phases in dielectrics with a structure of β-K2SO4. |
page 5 |
|
§ 1.1 Theory of phase transitions and incommensurate phases |
page 5 |
|
§ 1.2 Radiospectroscopic research methods Incommensurate modulated structures . |
page 16 |
|
§ 1.3 Experimental studies of compounds of the family A2BX4 type structure β-K2SO4. |
page 24 |
|
§ 1.4 The study of incommensurate phases in dielectric crystals at high pressure . |
page 34 |
|
Chapter 2. Equipment and measurement technique. |
|
|
§ 2.1 The sensitivity of the receiving sensor NQR and conditions for optimal matching of the measuring chamber . |
page 40 |
|
§ 2.2 Temperature consoles to a spectrometer for studies of phase transitions . |
page 45 |
|
§ 2.3 Synthesis samples |
page 49 |
|
§ 2.4 Apparatus for NQR studies under high hydrostatic pressure . |
page 50 |
|
Chapter 3. Sequence of phase transitions in compounds A2BX4 (X = J) |
|
|
§ 3.1 Phase transitions in Cs2CdJ4 . |
page 58 |
|
§ 3.2 Study the sequence of phase transitions in Cs2ZnJ4 . |
page 61 |
|
§ 3.3 NQR study of phase transitions in (NH4)2ZnJ4 . |
page 76 |
|
§ 3.4 Polymorphism in the family A2BX4 . |
page 82 |
|
Chapter 4, Sequence of phase transitions in Rb2ZnBr4 at atmospheric and high hydrostatic pressure |
|
|
§ 4.1 The absorption spectra of 79,81Br in the incommensurate phase at atmospheric pressure . . |
page 90 |
|
§ 4.2 PT phase diagram of Rb2ZnBr4 . . |
page 107 |
|
§ 4.3 Features conversion spectrum near TC. Comparison of diffraction data . |
page 131 |
|
§ 4.4 Discussion of the phase diagram of the model of "devil's staircase" . |
page 150 |
|
MAIN RESULTS. |
page 161 |
|
Conclusion . |
page 162 |
|
References . |
page 163 |
INTRODUCTION
Studies of the structure of the crystal structures, the nature of phase transitions recently reached a qualitatively new level. By theoretical and experimental work has been formulated a universal approach to the description of phase state on the basis of solving discrete field theory models. In the language of the theory of interacting nodes on harmonic lattice spins have been found and studied nonlinear solutions in the form of fermions. At the same time, as it turned out, the system can be represented by the normal fermion modes. The theory of the soft mode condensation Goldstounovskogo boson is just a special case of solutions in the form of single-particle fermion states - for example, the spin-wave or soliton.
Theoretical and experimental studies carried out for the external magnetic field and take into account only the spin-spin interaction in the framework of models with different dimensionality, showed that the behavior of the system depends not only on the spin and spatial dimension of the system, but must be considered a significant radius interspin interaction. It has been found that in this case there are classes of solutions to form the long-period structure, and observed experimentally.
In recent years, were discovered and studied compounds with charge density waves, quasi-one organic semiconductors and dielectrics, in which it was found ordering various elements of the structure similar to the long-period form of magnets.
Unlike magnetic systems in dielectric crystals at the forefront of the dipole-dipole interaction and the dimension of the spin variable gives way pseudospin ordering chemical bonds. In crystalline dielectrics with a structure of β-K2SO4 were first detected with an incommensurate phase, compared with the original sample intervals. From X-ray data indicated that the emerging superstructure reflections can be characterized by a temperature dependent parameter disparity.
Change the local environment of the structural units in phases with such features more optimal way to observe change of the electric field, or its constituents. Therefore, the method of nuclear quadrupole resonance (NQR) observed in the nucleus with the quadrupole moment and depends on the electric field gradient at the nucleus under study, is optimal for the study of incommensurate structures. Nucleus Cl, Br, J in crystals of the family A2BX4 occupy a convenient structural position and allow to obtain information about the origin of the primary structural disproportion, the type of phase transition, modulation features.
With the participation of the author have been made one of the first such studies, including those under the influence of high hydrostatic pressure. Involvement of the latter, as an additional parameter allows you to get a new non-trivial information about the incommensurate phase.
The objectives of this thesis include studies by nuclear quadrupole resonance of halogens (Cl, Br, J), and other methods, crystals family β-K2SO4 with structural disproportion. Elucidation of changes in the spectral features of the resonance parameters in phase transitions and symmetry transformations, the analysis of the local environment and the nucleus of its transformation into different compounds of this series with temperature and high hydrostatic pressure. Investigation of the processes of the spin dynamics. In combination with other methods of analysis of changes in the crystal symmetry at structural phase transitions.
Chapter 1. Incommensurately modulated phases in dielectrics with structure type β-K2SO4.
§ 1.1.Theory of phase transitions and incommensurate phases.
Phase transition is called structural when changes-crystallographic structure of matter. Symmetry of the crystal lattice, as it is known, in the general case described simorfnymi 230 space groups. Change in the symmetry of the crystal at the phase transition seemed, until recently, in the framework of the Landau-Devonshire, as a change of some function, called the order parameter, by the loss of the symmetry elements and decreasing the initial symmetry Go to a certain subgroup of the symmetry group G1 Go.
From the point of view of the atomic structure of the crystal, this means that the asymmetric atoms in the G1 phase, shifted relative to the equilibrium positions which they occupy at the high phase. The structure of the new phase G1 is a superposition of the displacements corresponding frozen soft mode and structure of G0 phase. Hence the structure of the new phase is uniquely determined by the structure of the initial phase and the vector of the soft mode (the symmetry of the soft mode).
According to Anderson's theory [1], phase transitions caused by the instability of the crystal relative to some of its normal modes in the high-temperature phase. The frequency of this mode decreases when approaching the critical temperature Ti, and the restoring force for displacements corresponding to such a fashion tends to zero as long as the phonon does not condense on the stability boundary. Consequently, the static displacements of atoms at the transition from phase G0 to G1 phase are frozen vibrational displacement codes corresponding to the soft phonon (qs).
However, this concept is applicable when the displacements of atoms from the high-small positions (phase transitions of bias) and becomes less useful for large displacements (phase transitions of the order-disorder).
In the latter case, structural changes are usually described in the framework of the Ising model, which deals with large-scale motions and entered the (pseudo) spin variables describing the position of atoms or groups. The results of this approach generally boil down to the fact that the phase transition occurs at the wave vector qs, which corresponds to a maximum of interactions J(q) between objects Ising nodes.
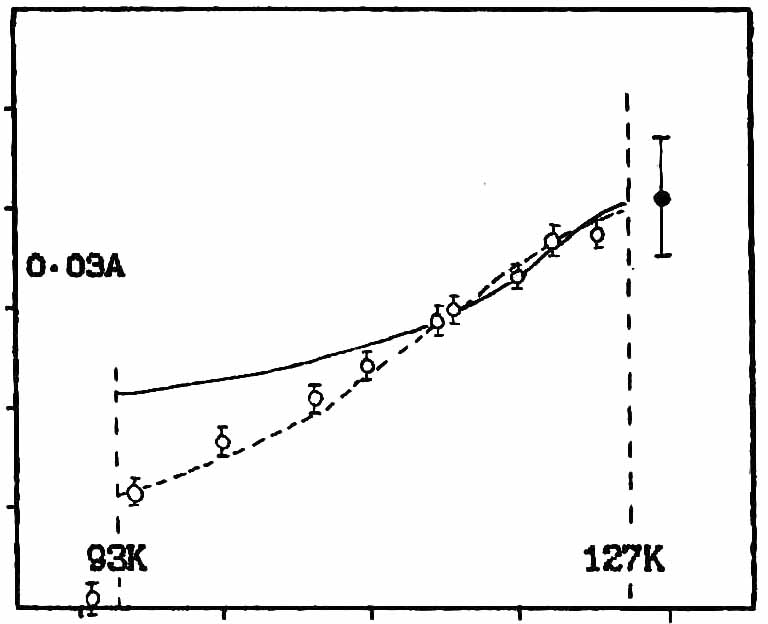
Parallel - the development of theory undertaken considerable experimental efforts to study the microscopic nature structure phase transitions. Most known results of the classical study of the temperature dependences of qs in β-K2SO4 [2]. Neytron - diffraction method on this crystal were shot dispersion curves q(ω) at different temperatures Figure 1.1. Temperature dependence of q for S2 fashion shows that the wave rector qs can have values between zero and the wave vector at the Brillouin zone boundary. In this case, the value qs, corresponding to a minimum the dispersion curve, the symmetry is not fixed and typically depends on the temperature.
Changes in the structure of the crystal in this case determined by the symmetry of high-G0 phase, followed by some pretransitional area corresponding mitigation fashion responsible for the phase transition at Ti. Below Ti there is a phase where the minimum of the soft mode varies near the symmetrical point of reciprocal space G*, and when they correspond exactly qs G*, at Tc transition occurs in the low-symmetry structure. The phase between Ti and Tc is called, incommensurat because values of the wave vector qs, when it is a continuous change can take irrational values, which corresponds to an infinitely large unit cell of the crystal. In this case the crystal is represented three-dimensionally periodic structure, where any inside – crystalline function in one or more directions superimposed long-wavelength spatial modulation period is generally not a multiple of the period of the unit cell of high-symmetry phase. Displacement of nucleus of symmetric function of the order parameter in this
0 0.5 qs 1.0 q
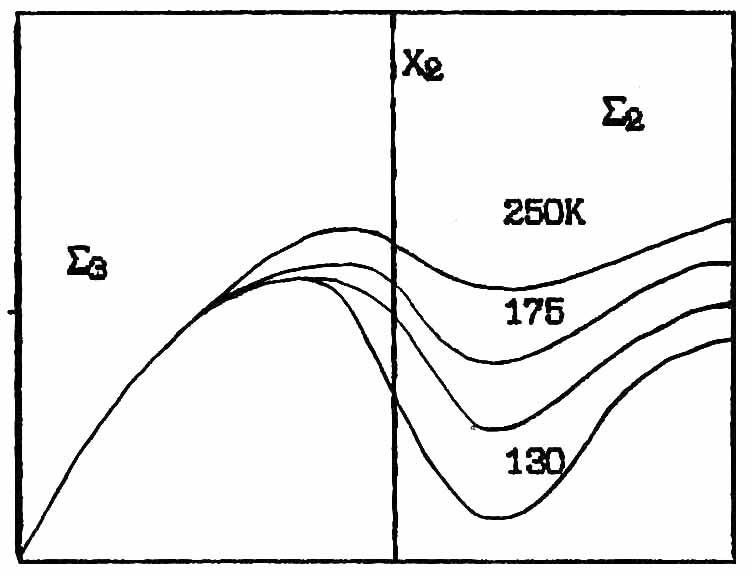 |
Figure 1.1. Dispersion curves for the soft mode in K2SeO4 at different temperatures and the dependence qs-1/3(1-δ)2π/a.
case, can be represented by an expansion in the eigenvectors of the soft mode [2,3]:
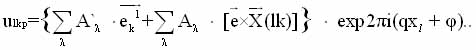 (1.1.)
(1.1.)
where ekl - eigen vectors irreducible representation G*; G*; А'l, Аl - amplitude eigenvectors; X (lk) – l-st position of the atom, the center of mass of k-th group in the p-th unit cell; j-wave phase modulation.
Analysis of the interaction of atoms in an external periodic potential shown [4,5] that the period of the structure is fixed on the true meaning and proportioned incommensurate phase is not realized. The resulting wave vector, depending on the "pressure", varies continuously, but Nonanalytic. For this strange behavior, mathematicians devised a very original name - "Devil's Staircase" (devil or Satan staircase) [5]. However, initially there was no hope to explore different types of non-analytic behavior numerically, and even more so by experiment.
In addition to the theory of Aubrey [5,6], in [7,8,9], to describe the transition from incommensurate (Jc) to the commensurate phase were introduced "domain" wall or soliton theory and developed the idea as part of Macmillan Ising models with solitons, phasons and "devil's staircase".
Results McMillan, reduced to the fact that the transition from JC in the commensurate phase can be represented by a picture of soliton-like structure of the atomic displacements described by the soliton (domain) wall :
u = A cosφ(x); φ(х) - k/p arctg(exp(-ax/p )) (1.2)
φ(х) = 2π/р; р = 1,2,...k.; These walls separate regions with different values of the phase shifts of atoms φ(х) = 2p/р; р = 1,2,...k.. Shape of the phase function in the incommensurate (incommensurate) phase is given by:
φ(х) = φо + φ(х-mb) (1.3)
where φо - the phase shift; b - distance between the walls, m = 1,2,3, ... p.
When the temperature decreases, the width of the soliton wall and a-1 is a continuous transition to the commensurate state. . Order parameter in this case is the number of solitons.
In real crystals, if the width of the soliton is a few lattice periods, the center of the soliton is energetically advantageous to have at some point in the unit cell [10]. In this case, the transition to the final as symmetrical, the system will experience a sequence of phase transitions of the first kind, until you reach the main phase with p = k. In addition, there are often a few stars of the wave vectors that lead to the existence of incommensurate walls of various types, and can be carried out transitions between different configurations of the soliton structure.
There are other types of non-linear numerical solutions (kinks, wobblers, etc.), describing the shape of the atomic displacements in the incommensurate phase. Such as NaNO2, the structure seems almost plane waves, and up to T C no harmonics incommensurate wave vector [11].
McMillan ideas were developed Janson[8] Aubrey [12]and Buck [13] These authors studied the behavior of soliton solutions of the discrete problem in Ising-like systems with the interaction up to three neighbors (ANNNI - model). In this case, the deviation of the wave vector qδ = (1- )*/3 proportioned values can be represented by a rational number x = M/N, and the structure of solutions (steps "devil's staircase") may be associated with symmetry interconnected sublattices with symmetry restrictions on the values of the numbers N and M. Then the transition from the high-G0 in the low-symmetry phase Gi, between the phase diagram there is a region where the structure is represented by a cascade of intermediate or long-period incommensurate states with discrete or continuous variation of the wave vector qδ (Fig.4.38 and 4.39). The regions of these states are very sensitive to external (theoretical) effects.
By this time the state of the theory of symmetry was enough to make its results for the classification of all possible types of theoretical incommensurate structures [15] and classify them into different classes incommensurate space groups in the theory of supersymmetry [16].
Supersymmetry transformation rules allow you to specify the direction of the transformation and permissible types of symmetry of incommensurate structures that can realistically be implemented in each class Fedorovskoye crystal structure.
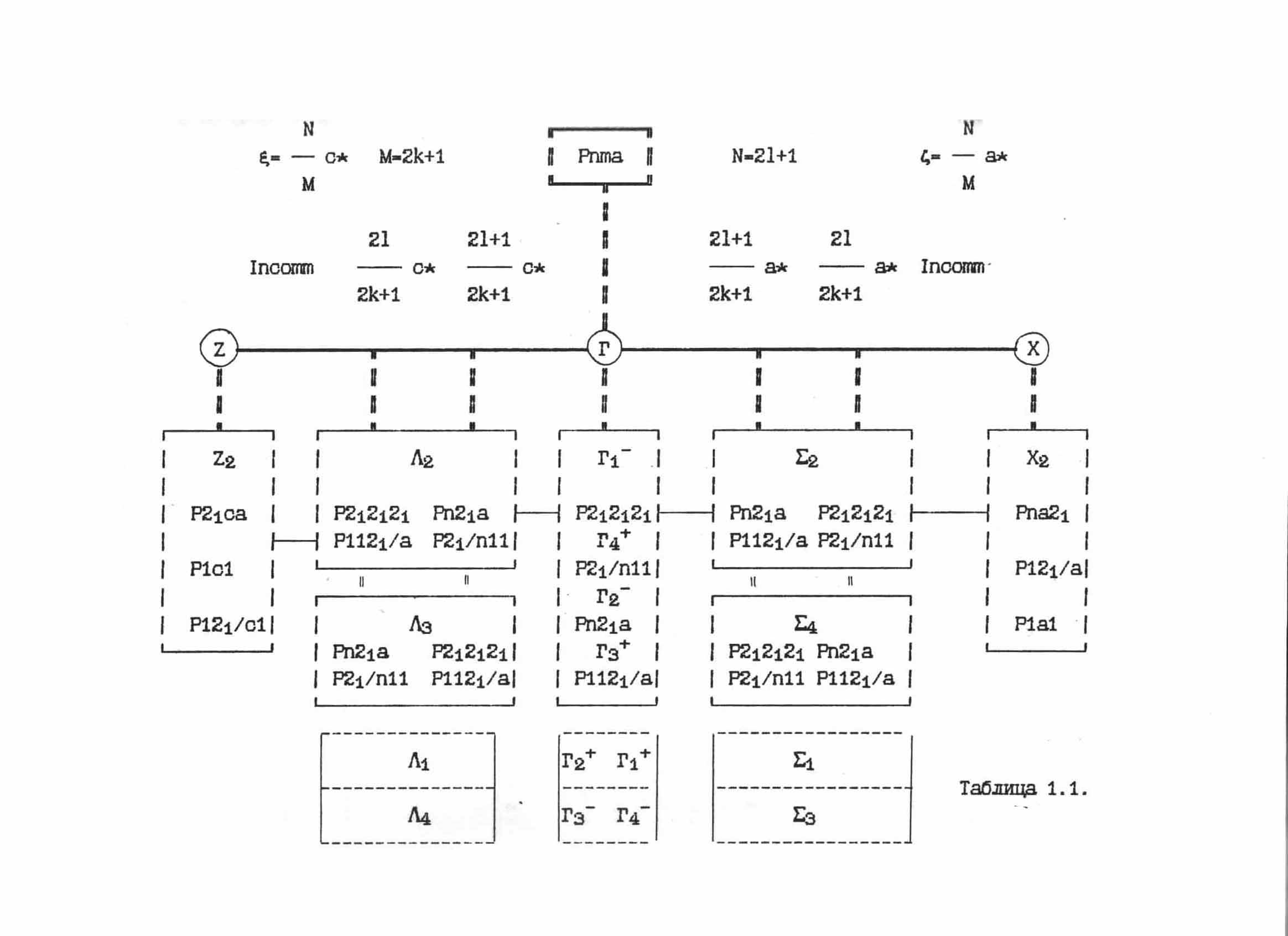
As an illustration, we give an outline of possible directions changes in lattice symmetry Brillouin highly symmetric group D2h16 (Pnma), Figure 1.2. In the circles of indexed figures experimentally realized soft modes for crystals 1) Tb2(Mo04)3, km = p (110) 2) RbD3(Se03)2, kz = p (001) 3) K2SeO4 , k = 2p (m00) m»1/3 In [18] is a diagram indicating the possible ways of symmetry transformations structure Pnma (D2h16).
From the experimental data revealed that the sequence of phase transitions in crystals with high-symmetry group symmetry Pnma structure β-K2SO4 defines mitigation dispersion curve along the S . line. There are four irreducible representations of S1, S2, S3, S4 of this group. In K2SeO4, for example, the soft mode associated with the representation of S2:
E-line E-line
(D2h16) (Pnma) ---------► Jc modulation --------►C2v9 (Pna21)
m»1/3 along the x-axis m»1/3
Later in other compounds of the family A2BX4 type structure β-K2SO4, installed other possible sequences of symmetry transformations, which are determined by another basis of irreducible representations of ![]() (Table 1.1).
(Table 1.1).
Given the possibility of experimental observation of the behavior of "devil's staircase" or to account for the influence of concomitant and secondary order parameters, the analysis of experimental structural data necessary to know the various ways allowed symmetry transformations of the structure, taking into account the parity ratio x= N/M in the case of long-period structures . The analysis performed in Refs [17, 18], which indicates all possible subgroups generated representations Si, Li, Gi
The above theory of solids based on the adiabatic or Born-Oppenheimer approximation, where the kinetic energy of the nucleus T (Rn) is actually neglected. However, as the last experimental studies [23], the characteristic times of nuclear motions can be compared with the electronic. Arise in this case, the vibronic interaction, even in the case of mixed singlet states, lead to Jahn-Teller distortions, which crystal system can be a source of instability and dipole explain the nature of ferroelectricity [22]. From the standpoint of the vibronic theory postulates soft mode are consequences of the cooperative pseudo-Jahn-Teller effect. In the framework of this theory can be explained and the disproportionate nature of the state in dielectric crystals. Interaction of the electron or nuclear state leads to interaction pseudo-soft phonon modes of different symmetry, localized near a variety of provisions of the reciprocal lattice symmetry [8, 94]. In the high-temperature phase G0, these modes do not interact, but below the temperature will determine the resonant interaction of the two components of the structure, phase-shifted.
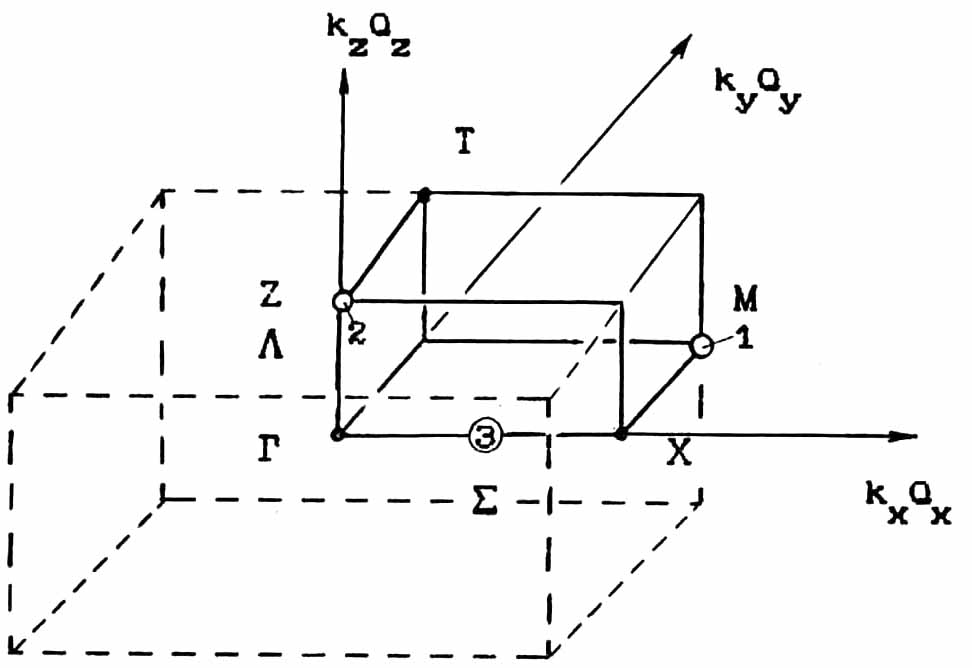
Figure 1.2. Symmetric points and directions of the lattice Brillouin grupy D2h16 (Pnma).
the standpoint of the atomic arrangement of this will lead to cooperation between the two sublattices of the crystal with different periods and realized a disproportionate or mosaic-cluster state.
Recently, efforts have been made to combine the universality hypothesis and cluster theory of phase transitions. In this way on the basis of experimental data for the theoretical foundations of association phase transitions of receiving and order-disorder [19,20]. There are reasonable grounds to believe that these transitions differ only in magnitude of the contribution from the phonon modes and pseudospin. This theory considers the equilibrium configurations of atoms in direct space:
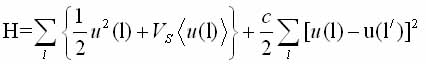 (1.4) with single-particle potential:
(1.4) with single-particle potential:
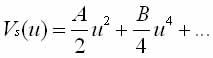
In contrast to the models discussed above is introduced varying degrees of anharmonicity motion near double-well potential. In the case where the value of g = V°s/kSTC (ratio of the depth of the pit to the local thermal energy) is small, the offset describes weakly damped mode, otherwise the soft mode From is strongly overdamped, and there is strong anharmonicity of the atomic motion in the potential Vs (g>l). In the latter case, at low temperatures (below TC) one of the holes has a large population. As numerical calculations before TC there Pretransitional area where there are buds (clusters), whose structure is similar to the structure of the low-temperature phase. Finite lifetime and size correlated moving clusters form different from that of the matrix, a dynamic structure, which is manifested in the spectral response function of the system. Molecular dynamics method were obtained solving the equations of motion with the Hamiltonian (4) as a nonlinear soliton solutions. In case of submission of solitons in the form of pseudo-ideal gas particles, the spectral function of the system is described as a phonon spectrum plus scattering due to slower movement of clusters (Gallo, diffuse bands on radiographs). When the speed of the cluster (or its borders) greater than the change in its size, there is a critical narrowing of the spectral components (central peak). Or, in the case of bias, if the fluctuations around quasi offset provisions are large compared with the quasi-equilibrium by the local displacements.
Even for small fluctuations in the presence of correlated moving regions should lead to redistribution contribution to the spectral response function between the quasi-harmonic frequencies and part responsible for the cluster scale movement.
Thus, even if the bias (g « 1), the spectral function of the coordinate ordering Q completely changed at Ti> TC with decreasing T. For T <Ti soft phonon spectrum into the growth of the central peak. In systems offset soft mode has a resonant nature, although it may be a bit muted (Re and Im parts different from zero). In systems of order-disorder imaginary part of the soft mode is always different from zero, a Re part only if the quantum mechanical ground state splitting (tunneling, H-bonds). Cluster pattern in the transition of the displacement type allows crossover from mode to mode bias order-disorder at T> Tc, as a result of the coherence of atomic motions.
Temporal and spatial correlation functions of clusters, also have considerable scale range. Maximum size and lifetime limited correlation length and time, and the minimum value - the size of embryos and their lifetime in development threshold temperature fluctuations. If the system causes an increase in the size of preventing germs зародышей time structural redistribution could increase significantly and experimentally observed complete or partial freezing of non-equilibrium state of the system (windows). In the thermodynamic sense, the surface free energy of the system in the microscopic space of external parameters is represented by many local minimums separated by high energy barriers which may exist for a long time long-lived metastable phases overlapped with the topological structure (quasi-ergodic behavior) [21].
The problem of implementation of some elements of the crystal structure in a state such as glass, under quasiergodic assumptions led to the development of new approaches in the thermodynamic description of phase transitions. Quasiergodic system under certain conditions can evolve different structural time-dependent pathways in megascopic (cluster) and the macroscopic sense. In this case also, there is certain temperature Тк, the separating region with various types of thermodynamic behavior.
English abstract Avtoreferat § 1.1 § 1.2 §1.3 § 1.4 § 2.1 § 2.2 §2.3 §2.4 § 3.1 § 3.2 § 3.3 § 3.4 § 4.1 § 4.2 § 4.3 § 4.4 Reference Template pdf abstract
tags for search: phase transitions and incommensurate phases in A2BX4 , Cs2ZnJ4 , (NH4)2ZnJ4 Cs2CdJ4 ; P-T phase diagram of Rb2ZnBr4 ; devil's staircase .