Диссертация автореферат оглавление §1.1 §1.2. §1.3 §1.4 §2.1 §2.2-4 §3.1-2 §3.3-4 §4.1 § 4.2. § 4.3 §4.4 заключение ссылки
pdf: Глава 1 Глава 2 Глава 3 Глава 4 Библиография Диссертация вся pdf English pdf
ВВЕДЕНИЕ
Исследования строения кристаллических структур, природы фазовых переходов за последнее время вышли на качественно новый уровень. Благодаря теоретическим и экспериментальным работам был сформулирован универсальный подход к описанию фазового состояния на основе решения дискретных моделей теории поля. На языке теории взаимодействующих на узлах гармонической решетки спинов были обнаружены и исследованы нелинейные решения в виде фермионов. При этом, как оказалось, система может быть представлена нормальными фермионными модами. Теория мягкой моды, конденсация Гольдстоуновского бозона, является лишь частным случаем решения в виде одночастичного фермионного состояния - например, солитона или спиновой волны.
Теоретические и экспериментальные исследования, выполненные для магнетиков во внешнем поле и учитывающие только спин-спиновое взаимодействие в рамках моделей с различной размерностью, показали, что поведение системы определяется не только спиновой и пространственной размерностью системы, но необходимо учитывать значительный радиус межспинового взаимодействия. Было установлено, что в этом случае имеются классы решений в виде длинно-периодических структур, наблюдаемых и экспериментально.
В последнии годы были открыты и исследованы соединения с волнами зарядовой плотности, квазиодномерные органические полупроводники и диэлектрики, в которых было обнаружено упорядочение различных элементов структуры схожее с длиннопериодической формой магнетиков.
В отличии от магнитных систем в диэлектрических кристаллах на первый план выходит диполь-дипольное взаимодействие и размерность спиновой переменной уступает место псевдоспиновому упорядочению химических связей. В кристаллических диэлектриках со структурой типа β-K2SO4 впервые были обнаружены фазы с несоразмерной, по сравнению с исходной, периодичностью образца. Из рентгеноструктурных данных следовало, что появляющиеся сверхструктурные рефлексы могут характеризоваться температурно зависимым параметром несоразмерности.
Изменение локального окружения структурных единиц в фазах с такими особенностями оптимальнее всего наблюдать по изменению электрического поля, либо его составляющих. Поэтому метод ядерного квадрупольного резонанса (ЯКР), наблюдаемый на ядрах с квадрупольным моментом и зависящий от градиента электрического поля на исследуемом ядре, является оптимальным при исследовании несоразмерных структур. Ядра Cl, Br, J в кристаллах из семейства А2ВX4, занимают удобное структурное положение и позволяют получить первичную информацию о возникновении структурной несоразмерности, типе фазового перехода, особенностях модуляции.
С участием автора были выполнены одни из первых подобных исследований, в том числе и под воздействием высокого гидростатического давления. Привлечение последнего, как дополнительного параметра, позволяет получить новую нетривиальную информацию о несоразмерной фазе.
В задачи данной диссертации включены исследования методом квадрупольного резонанса ядер галогенов (Cl, Br, J), и другими методами, кристаллов семейства β-K2SO4 со структурной несоразмерностью. Выяснение особенностей изменения спектральных параметров резонанса при фазовых переходах, преобразований симметрии, анализ локального окружения исследуемых ядер и его трансформации в различных соединениях этого ряда при изменении температуры и высокого гидростатического давления. Исследование процессов спиновой динамики. В комплексе с другими методами анализ изменения симметрии кристаллов при структурных фазовых переходах.
Глава 1. Несоразмерно модулированные фазы в диэлектриках со структурой типа β-K2SO4.
§1.1. Теории фазовых переходов и несоразмерные фазы.
Фазовый переход принято называть структурным, когда изменяется-кристаллографическая структура вещества. Симметрия кристаллической решетки, как известно, в общем случае описывается 230 симорфными пространственными группами. Изменение симметрии кристалла при фазовом переходе представлялось, до недавних пор, в рамках теории Ландау-Девоншира, как изменение, некой функции, называемой параметром порядка, путем утраты части элементов симметрии и понижением первоначальной симметрии Go до симметрии некоторой подгруппы G1 группы Go.
С точки зрения атомной структуры кристалла это означает, что атомы в несимметричной фазе G1, смещены относительно равновесных положений, занимаемых ими в высокосимметричной фазе. Структура новой фазы G1, является суперпозицией смещений, отвечающих замороженной мягкой моде и структуре фазы G0. Следовательно структура новой фазы однозначно определяется структурой исходной фазы и вектором мягкой моды (симметрией мягкой моды).
Согласно теории Андерсона [1], фазовые переходы вызваны неустойчивостью кристалла относительно некоторых его нормальных мод в высокотемпературной фазе. Частота этой моды уменьшается при приближении к критической температуре Ti, а восстанавливающая сила для смещений, отвечающих такой моде, стремится к нулю до тех пор, пока фонон не конденсируется на границе устойчивости. Следовательно, статические смещения атомов при переходе из фазы G0 к G1 фазе представляют собой замороженные смещения колебательной коды, отвечающей мягкому фонону (qs).
Однако, такая концепция применима, когда смещения атомов из высокосимметричных положений малы (фазовые переходы типа смещения) и становится менее полезной при значительных смещениях (фазовые переходы типа порядок-беспорядок).
В последнем случае структурные преобразования принято описывать в рамках моделей Изинга, где рассматриваются крупномасштабные движения и вводятся (псевдо)спиновые переменные, описывающие положение атомов или их групп. Результаты этого подхода в общем виде сводятся к тому, что фазовый переход осуществляется при волновом векторе qs, которому отвечает максимум взаимодействий J(q) между объектами изинговских узлов.
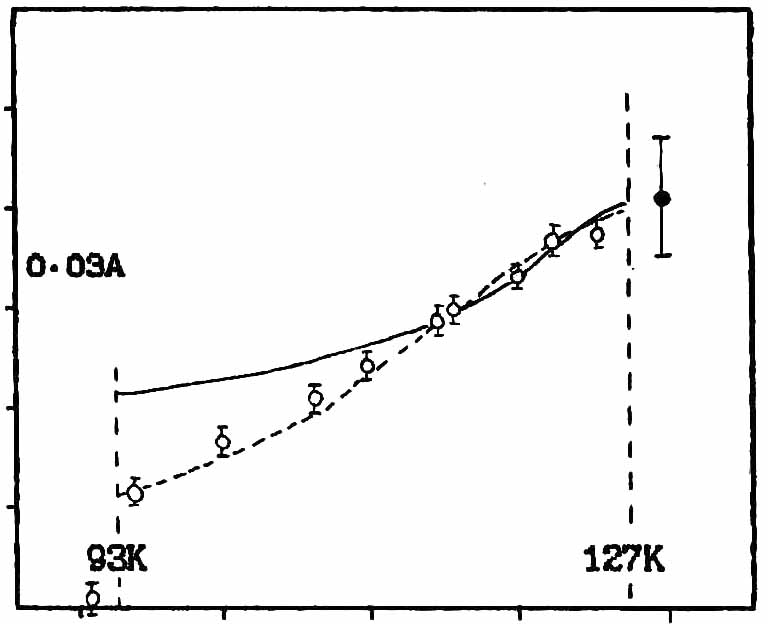
Параллельно - развитию теории предпринимались значительные экспериментальные усилия по изучению микроскопической природы сруктурных фазовых переходов. Наиболее известны результаты классического исследования температурных зависимостей qs в β-K2SO4 [2]. Методом нейтроновской дифракции на этом кристалле были отсняты дисперсионные кривые q(ω) при разных температурах Рис.1.1. Температурная зависимость q для S2 моды указывает, что волновой ректор qs может иметь значения между нулем и волновым вектором на Границе зоны Бриллюэна. В этом случае значение qs, отвечающее минимуму дисперсионной кривой, не фиксировано симметрией и обычно зависит от температуры.
Изменение структуры кристалла в этом случае определяется симметрией высокотемпературной фазы G0, после которой следует Некоторая предпереходная область, соответствующая смягчению моды, ответственной за фазовый переход при Ti. Ниже Ti имеется фаза, где минимум мягкой моды изменяется вблизи симметричной точки обратного пространства G*, и, когда qs точно соответствует G*, при Тc происходит переход в низкосимметричную структуру. Фаза между Ti и Тc получила название, несоразмеренной, т.к. значения волнового вектора qs, при его непрерывном изменении, могут принимать иррациональные значения, что соответствует бесконечно большой элементарной ячейке кристалла. В этом случае кристалл представляется трехмерно-периодической структурой, где на какую-либо внутри кристаллическую функцию в одном или нескольких направления наложена длинноволновая пространственная модуляция, период которой в общем случае не кратен периоду элементарной ячейки высокосимметричной фазы. Смещение ядер от симметричных положений и функция параметра порядка, в этом случае, могут быть представлены разложением по собственным векторам мягкой моды [2,3]:
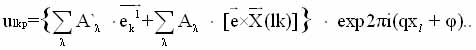 (1.1.)
(1.1.)
где еkl - собственные вектора неприводимого представления G*; А'l, Аl, - амплитуды собственных векторов;
hw, Мэв
0 0.5 qs 1.0 q d (в ед. а*)
 |
1.0
0.04
0.02
Рис.1.1. Дисперсионные кривые для мягкой моды в K2SeO4 при различных температурах и зависимость qs-1/3(1-δ)2π/a
X(lk) - положение 1-го атома, относительно центра масс k-ой группы, в р-ой элементарной ячейке; φ -фаза волны модуляции.
Анализ взаимодействия атомов во внешнем периодическом потенциале показал [4,5], что период структуры закрепляется на соразмеренном значении и истинно несоразмеренная фаза не реализуется. Результирующий волновой вектор, в зависимости от "давления", изменяется непрерывно, но неаналитически. Для этого странного поведения, математики придумали очень оригинальное название - "Devil's Staircase" (дьявольская или сатанинская лестница) [5]. Однако первоначально не было надежды исследовать различные типы не аналитического поведения численно, и тем более с помощью эксперимента.
В дополнение к теории Обри [5, 6], в работах [7, 8, 9], для описания перехода от несоразмеренной (J0) к соразмерной фазе были введены ↔доменные» стенки или теория солитонов и развита идея Макмиллана в рамках моделей Изинга с солитонами, фазонами и "чертовой лестницей".
Результаты Макмиллана, сводятся к тому, что переход из Ic в соразмерную фазу можно представить через солитоно-подобную картину смещений атомов структуры, описываемую солитонной (доменной) стенкой:
u = A cosφ(x); φ(х) - k/p arctg{ exp(-ax/p )} (1.2)
Эти стенки отделяют области с разными значениями фазовых сдвигов атомов φ(х) = 2π/р; р = 1,2,...k. Форма фазовой функции в несоизмеримой (несоразмерной) фазе определяется выражением:
φ(х) = φо + φ(х-mb) (1.3)
где φо - фазовый сдвиг; b - расстояние между стенками, m = 1,2,3,...р.
При уменьшении температуры уменьшается ширина солитонной стенки a-1 и происходит непрерывный переход в соразмерное состояние. Параметром порядка в этом случае является число солитонов.
В реальных кристаллах, если ширина солитона составляет несколько периодов решетки, центру солитона энергетически выгодней располагаться в определенной точке элементарной ячейки [10]. В этом случае, при переходе к конечному симметричному состоянию, система будет испытывать последовательность фазовых переходов первого рода, пока не будет достигнута основная фаза с р = k. Кроме того, часто имеется несколько звезд волновых векторов, обуславливающих существование несоразмерных стенок различных типов, и могут осуществляться переходы между различными конфигурациями солитонной структуры.
Имеются и другие виды нелинейных численных решений (кинки, вобблеры и др.), описывающих форму смещений атомов в несоразмерной фазе. Например в NaNO2, структура представляется почти плоскими волнами, и вплоть до ТC отсутствуют гармоники несоизмеримого волнового вектора [11].
Идеи МакМиллана были развиты Янсоном [8], Обри [12] и Баком [13]. Эти авторы исследовали поведение солитоноподобных решений в дискретной задаче Изинго-подобных систем с учетом взаимодействия до третьих соседей (ANNNI - модели). В этом случае величина отклонения волнового вектора qδ = (1-d)с*/3 от соразмеренного значения может быть представлена с помощью рационального числа x=M/N, а структура решений (ступеней "чертовой лестницы") может быть связана с симметрией взаимосвязанных подрешеток, с симметрийными ограничениями на значения чисел N и М. Тогда при переходе из высокосимметричной G0 в низкосимметричную фазу Gi, между ними на фазовой диаграмме имеется область, где структура представлена каскадом промежуточных длиннопериодических или несоразмерных состояний с дискретным или непрерывным изменением волнового вектора qδ (Рис.4.38 и 4.39). При этом области существования этих состояний очень чувствительны к внешнему (теоретическому) воздействию.
К этому времени состояние теории симметрии было достаточным, чтобы приложить ее результаты для классификации всевозможных теоретических типов несоразмерных структур [15] и систематизировать их по различным классам несоразмеренных пространственных групп в рамках теории суперсимметрии [16].
Правила преобразования теории суперсимметрии позволяют указать направления преобразования и допустимые типы симметрии несоразмерных структур, которые могут быть реально реализованы в каждом Фёдоровском классе кристаллической структуры.
В качестве иллюстрации приведем схему возможных направлений изменения симметрии для решетки Бриллюэна высокосимметричной группы D2h16(Pnma), Рис.1.2. В кружочках индексированных цифрами экспериментально реализуются мягкие моды для кристаллов 1) Тb2(Мо04)3, km = p(110) 2) RbD3(Se03)2, kz = p(001) 3) K2SеО4, k = 2p(m00) m≈1/3. В работе [18] представлена схема указывающая пути возможных симметрийных преобразований структуры Pnma(D2h16).
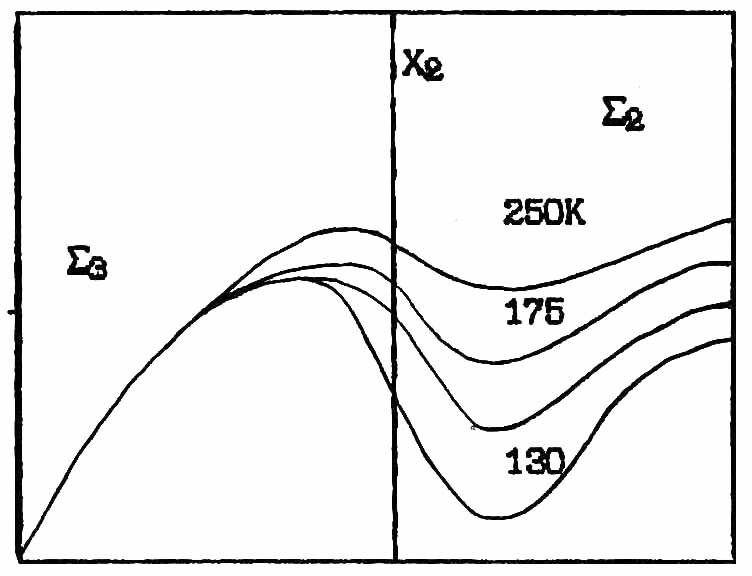
Из экспериментальных данных установлено, что последовательность фазовых переходов в кристаллах с высокосимметричной группой симметрии Pnma со структурой β-K2SO4 определяется смягчением дисперсионной кривой вдоль Σ линии. Имеется четыре неприводимых представления Σ 1, Σ 2, Σ 3, Σ 4 этой группы. В K2SеО4,например, мягкая мода связывается с представлением Σ 2:
Σ-line Σ-line
(D2h16)(Pnma) ---------⇒ Jc модуляция --------⇒ C2v9(Pna21)
μ≈1/3 вдоль оси х μ≈1/3
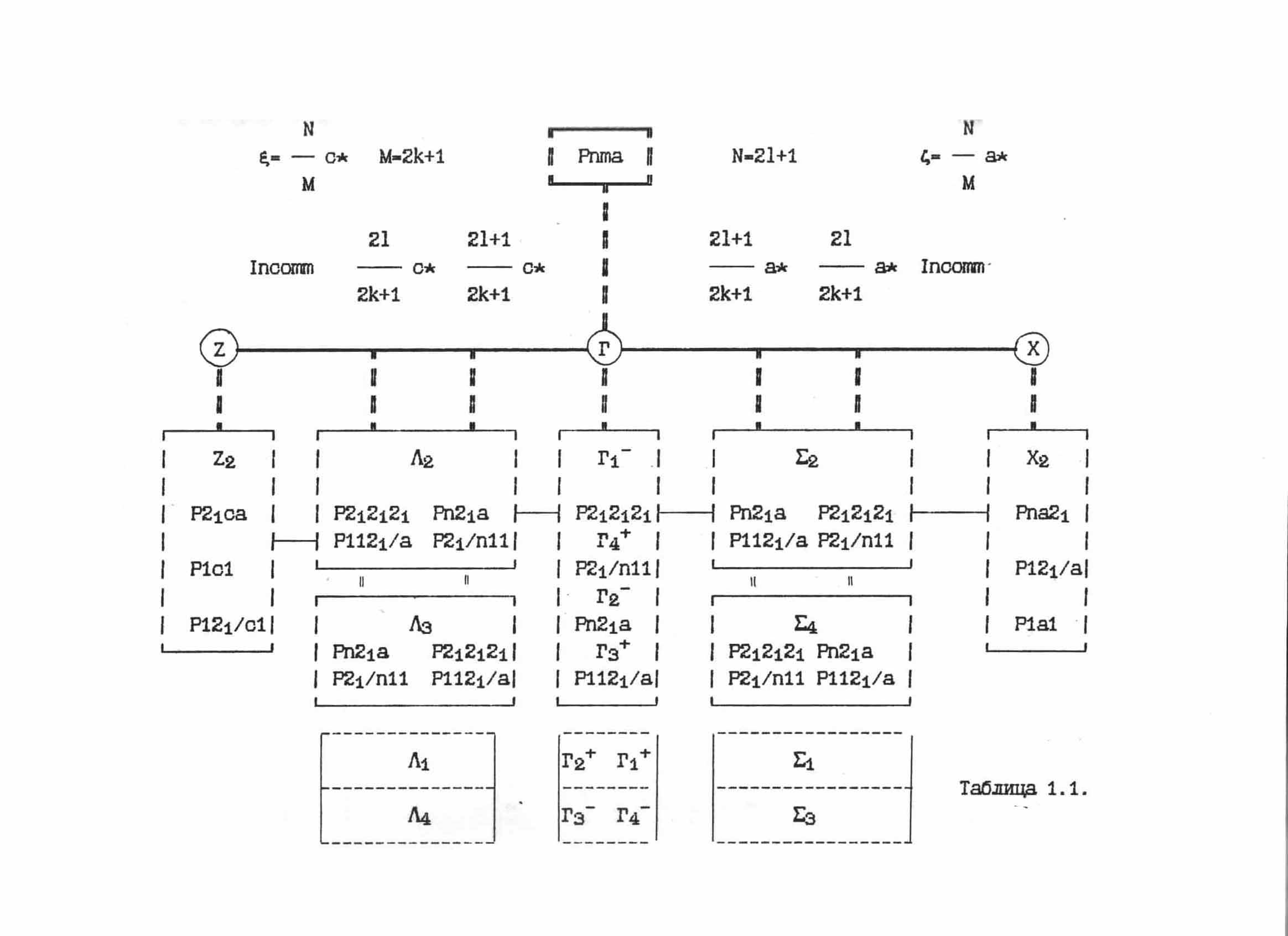
Позже в других соединениях семейства А2ВX4 со структурой типа β-K2SO4, были установлены другие возможные последовательности преобразования симметрии, которые определяются другим базисом неприводимых представлений группы D2h16 (Табл. 1.1).
С учетом возможности экспериментального наблюдения поведения типа "дьявольская лестница" или для учета влияния сопутствующих и вторичных параметров порядка, при анализе экспериментальных структурных данных необходимо знать всевозможные разрешенные симметрией пути преобразования структуры, с учетом четности или нечетности отношения x = N/M в случае длиннопериодических структур. Анализ выполненный в работах [17,18], указывает все возможные подгруппы генерируемые представлениями Si, Li, Gi
Вышеупомянутые теории твердого тела основаны на адиабатическом или Борна-Оппенгеймера приближении, когда кинетической энергией ядер T(Rn) фактически пренебрегают. Однако, как показывают последний экспериментальные исследования [23], характеристические времена ядерных движений могут быть сравнимы с электронными. Возникающие в этом случае вибронные взаимодействия, даже в случае смешанных синглетных состояний, приводят к Ян-Теллеровским искажениям, которые в кристаллической системе могут явиться источником дипольной неустойчивости и объяснить природу сегнетоэлектричества[22]. С точки зрения вибронной теории постулаты мягкой моды являются следствиями кооперативного псевдо-эффекта Яна-Теллера.
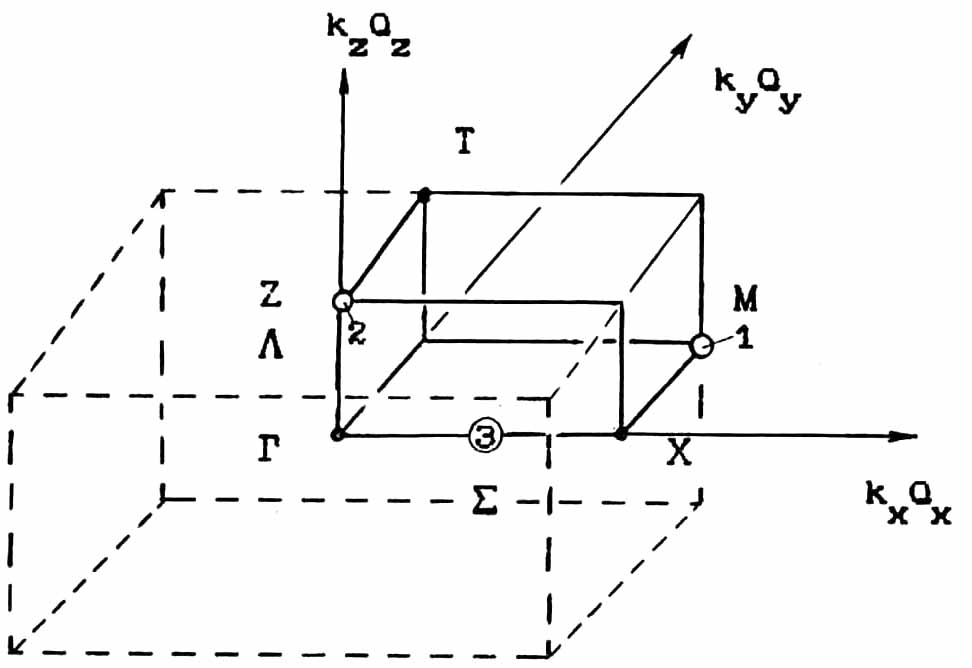
Рис.1.2. Симметричные точки и направления решетки Бриллюэна групы D2h16 (Pnma).
Таблица 1.1.
В рамках этой теории может быть объяснена и природа несоразмерного состояния в диэлектрических кристаллах. Взаимодействие электронных или ядерных состоянии приводит к взаимодействию псевдомягких фононных мод разной симметрии, локализующихся вблизи различных симметрийных положений обратной решетки [8,94]. В высокотемпературной фазе G0 эти моды не взаимодействуют, но ниже по температуре резонансное взаимодействие будет определять две компоненты структуры, смещенные по фазе. С точки зрения атомного расположения это приведет к взаимодействию двух подрешеток кристалла с разными периодами и реализуется несоразмерное или мозаично-кластерное состояние.
В последнее время предпринимаются усилия для объединения гипотезы универсальности с кластерной теорией описания фазовых переходов. На этом пути на базе экспериментальных данных заложены основы для теоретического объединения фазовых переходов типа вмещения и типа порядок-беспорядок [19,20]. Появились весомые основания считать, что эти переходы различаются лишь по величине вклада от фононных и псевдоспиновых мод. Данная теория рассматривает равновесные конфигурации атомов в прямом пространстве:
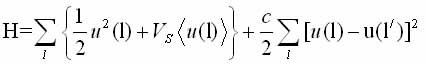 (1.4)
(1.4)
с одночастичным потенциалом:
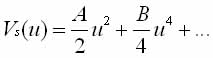 (1.5)
(1.5)
- u(l) - параметр порядка.
В отличии от моделей рассмотренных выше вводится различной степени ангармоничность движения вблизи двухминимумного потенциала. В случае когда величина g = V°s/kSTC (отношение глубины локальной ямы к тепловой энергии) мала, смещение описывается слабозатухающей модой, в противоположном случае мягкая мода сильно передемпфирована, и наблюдается сильно ангармоничное движение атомов в потенциале Vs(g>l). В последнем случае при низких температурах (ниже ТC) одна из ям имеет большую населенность. Как показывают численные расчеты,перед ТC существует предпереходная область, где возникают зародыши (кластеры), структура которых подобна структуре низкотемпературной фазы.
Конечное время жизни и размер скоррелировано движущихся кластеров образуют, отличную от матричного, динамическую структуру, которая проявляется в спектральной функции отклика системы. Методом молекулярной динамики были получены решения уравнений движения с гамильтонианом (4) в виде солитоноподобных нелинейных решений. В случае представления солитонов в виде идеального газа псевдорелятивистских частиц, спектральная функция системы описывается в виде фононного спектра плюс рассеяние обусловленное более медленным движением кластеров (галло, диффузные полосы на рентгенограммах). Когда скорость кластера (или его границы) больше величины изменения его размеров, наблюдается критическое сужение данной спектральной компоненты (центральный пик). Или, в случае смещения, если флуктуации около смещенных квазиравновесных положений велики по сравнению с самими локальными квазиравновесными смещениями.
Уже при небольших флуктуациях, наличие скоррелированно движущихся областей должно приводить к перераспределению вклада в спектральную функцию отклика между квазигармонической частью и частотами ответственными за кластерный масштаб движения.
Таким образом даже в случае смещения (g « 1) спектральная функция координаты упорядочения Q совершенно изменяется при Тi > ТC при понижении Т. Для Т < Ti мягкофононный спектр переходит в рост центрального пика. В системах смещения мягкая мода имеет резонансную природу, хотя и может быть немного демпфирована (Re и Im части отличны от нуля). В системах порядок-беспорядок мнимая часть мягкой моды отлична от нуля всегда, a Re часть лишь при наличии квантово-механического расщепления основного состояния (туннелирование, H-связи). Кластерная картина при переходе типа смещения допускает кроссовер от режима смещения к режиму порядок-беспорядок при Т>Тc, как результат когерентности атомных движений.
Временные и пространственные корреляционные функции кластеров также имеют существенный масштабный диапазон. Максимальный размер и время жизни ограничено корреляционными длиной и временем, а минимальные значения - размером зародышей и временем их жизни при пороговой температуре развития флуктуации. При наличии в системе причин препятствующих увеличению размеров зародышей, время стукуктурного перераспределения может значительно увеличиться и экспериментально наблюдается полное или частичное замораживание неравновесного состояния системы (стекла). В термодинамическом смысле поверхность свободной энергии системы в микроскопическом пространстве внешних параметров представлена множеством локальных мимумов, разделенных высокими энергетическими барьерами, где длительное время могут существовать долгоживущие метастабильные фазы с перекрытой топологической структурой (квазиэргодическое поведение) [21].
Проблема реализации некоторых элементов структуры кристалла в состоянии типа стекла, в рамках квазиэргодического предположения привела к разработке новых термодинамических подходов при описании фазовых переходов. Квазиэргодическая система при некоторых условиях может эволюционировать различными структурными, зависящими от времени путями, как в мегаскопическом (кластерном), так и макроскопическом смысле. В этом случае также имеется некоторая температура Тк, разделяющая области с различным типом термодинамического поведения.
Диссертация автореферат оглавление §1.1 §1.2. §1.3 §1.4 §2.1 §2.2-4 §3.1-2 §3.3-4 §4.1 § 4.2. § 4.3 §4.4 заключение ссылки
pdf: Глава 1 Глава 2 Глава 3 Глава 4 Библиография Диссертация вся pdf English pdf