§ 4.4 Обсуждение фазовых диаграмм в рамках теоретических моделей "дьявольской лестницы".

   В заключении мы представим обобщенную экспериментальную Р-Т диаграмму Rb₂ZnBr₄ по данным ЯКР (Рис.4.35) и сравним её с теоретическим фазовым диаграммам полученными численными методами. Расчеты выполненные в [15,12,121] основаны на анизотропной модели Изинга с учетом взаимодействия до третьих соседей. Нас будет интересовать та часть фазовой диаграммы, где реализуются структуры с периодом близким к 1/3 и 1/4 Рис.4.38а. На этой диаграмме величине q_δ=l/3 соответствует конфигурация спинов <12> (один вверх, два вниз), q_δ=l/4-<121>, q_δ=5/17-<1121212(12)²>; q_δ=3/10-<112(12)²> и т.д. Если на этой диаграмме провести штриховую линию, как указанно на Рис.4.38а, и соотнести ее с экспериментальной шкалой температуры при атмосферном давлении, то, находящаяся выше этой линии часть фазовой диаграммы [121], окажется достаточно сравнимой с экспериментальной Р-Т диаграммой полученной нами. При этом с переходом к модификации этой модели в рамках псевдо-спиновых переменных [12] область существования структур с различными конфигурациями может изменяться (Рис.4.38б).

  Несколько другой подход разработан в последние годы [12]. В его основу заложена одна из модификаций параболической модели Френкеля-Канторовой и введен несиморфный элемент симметрии, в роли которого выступает нелинейная часть поляризации, осуществляющая связь между подрешетками. С увеличением вклада нелинейной поляризации Р_NL., в структуре с симметрией ряда Pnma, доли фаз 1/3 и 1/4, соответственно уменьшаются и увеличиваются, между ними появляются структуры низшего порядка симметрии (Рис.4.39). На увеличенной вставке части Рис.4.39 приведена часть диаграммы Обри, которая может быть сопоставлена с нашей фазовой Р-Т диаграммой.

  При рассмотрении области существования фазы 2/7, находящейся между фазами 1/3', 1/4'' фазовой диаграммы Обри и линий разделяющей фазы 1/3', 1/3 и 5/17 мы можем представить, что в нашем случае наблюдается более тонкая структура этих областей (как представлено на Рис.4.39б),

 

 

 

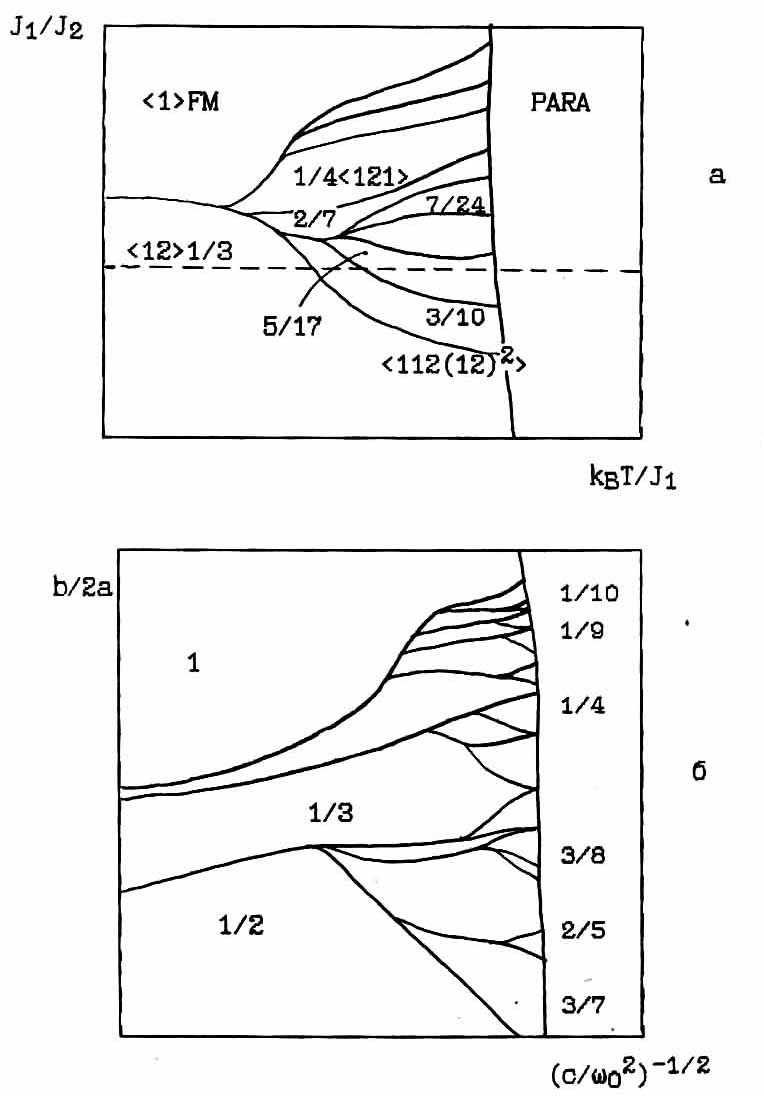
Рис.4.38    а) теоретическая диаграмма Селка [121];   б) фазовая диаграмма Обри [5].

 

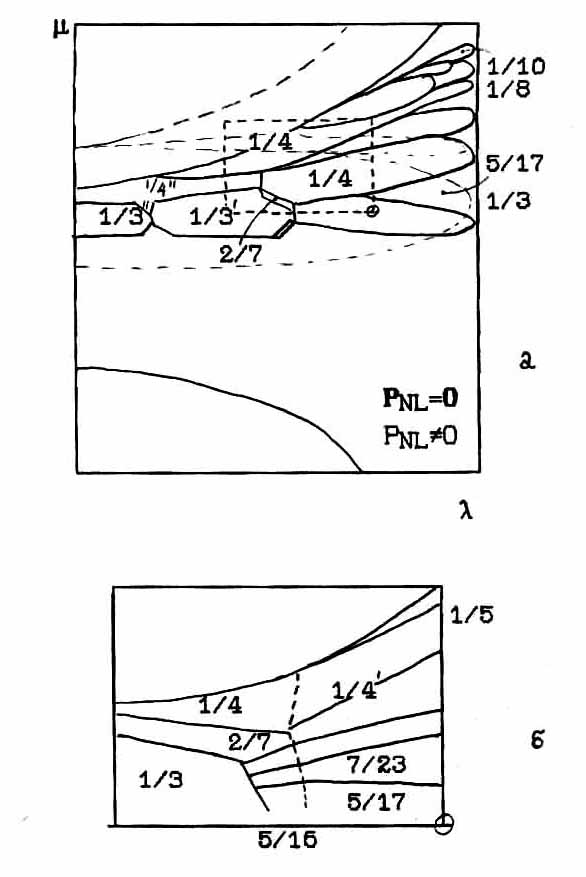
Рис.4.39.   Теоретическая фазовая диаграмма поляризационной    модели Обри [12].

 в виде ступеней промежуточных между 1/3 и 5/17 и между 5/17 и 2/7. В этом случае фазовая диаграмма RZB полученная методом ЯКР с учетом значений волновых векторов, измеренных нейтроновской дифракцией, хорошо сравнивается с теоретической фазовой диаграммой в модели Обри [12].

Как следует из многочисленных данных по экспериментальному исследованию фазовых диаграмм различных систем с фрустрирующими взаимодействиями, усложнение диаграмм происходит не только в случае учета более дальних соседей поперек оси анизотропии системы, но и с введением структурного беспорядка (случайного поля). Последнее может быть обусловлено примесями, H₂-связями, ядерной изотопией, а также наличием в кристалле прослоек или поверхностных фаз другой структуры. Опуская, однако, обсуждение неэргодичеокого [124,21] и скейлинга [123] типа поведения, которые могут наблюдаться в этом случае, мы остановимся на рассмотрении причин приводящих к стохастическому режиму, отмечаемому в приложениях двух- и трехразмерных ANNNI моделях [13]. Если, например, энергия системы близка к случаю утроения элементарной ячейки (или φ ≈ π/3), то структура в среднем является топологическим сочленением салитонов и антисолитонов в их случайной комбинации. В зависимости от параметров взаимодействия, некоторые комбинации будут энергетически более благоприятными. Такие хаотические фазы будут метастабильными, причем степень метастабильности зависит от связи параметра несоразмерности с упругой энергией. Бесконечное (или конечное) число стабильных состояний из набора "чертовой" лестницы могут быть разделены энергетическими барьерами и реальная система не сможет релаксировать к основному состоянию за конечное время.

В этом режиме существует два случая: слабый и сильный потенциал взаимодействия [13,120]. В этом, случае, когда расстояние между солитонами небольшое, несоразмерная фаза стабильна. При увеличении расстояния между солитонами, отталкивающее взаимодействие между ними не может преодолеть пиннинг решетки и наблюдается мягкий хаотический режим. При значительном превышении несоразмерного периода по сравнению с периодом решетки, стабилизируется высокотемпературная фаза. Здесь возможно поведение сходное с предпереходным кластерным упорядочением.

 При усилении связи между подрешетками ANNNI модели (сильный потенциал) ширина хаотического режима может сильно увеличится, а несоразмерная фаза станет состоянием включающим несколько длиннопериодических фаз. Так, например, вместо фазы q=2π/4(l-q_δ) в интервале волновых векторов q±Δq возможно четыре состояния модуляции q=3/16 = 1/4(1-1/4). Фазы будут различаться величиной фазового сдвига φ= φ₀ ± Δφ    близкого к π/4. При этих четырех длиннопериодических будут существовать две хаотические фазы. При уменьшении величины волнового вектора числа энергетически близких фаз будет увеличиваться. Каждая несоразмерная фаза будет представлена набором хаотических и длиннопериодических фаз. В этом случае должен наблюдаться сглаженный (incomplete) режим Devil's starcase', в отличии от чисто хаотического режима, где волновой вектор изменяется согласно классическому (smooth) режиму Devil's starcase'. В этом случае (для больших значений периода несоразмерности) истинно несоразмерная фаза не реализуется.

 Чтобы проанализировать такую возможность в нашем случае, мы, с [120], должны обратится к структуре Pnma. Как известно, в структуре А₂ВX₄ типа β-K₂SO₄ в некотором слое ab-плоскости центры тяжести двух ВX₄ тетраэдров расположены на том же уровне как и ион А (Рис.3.14). Между слоями z=l/4 и z=3/4 находятся оставшиеся А ионы. Если рассматривать структуру в пределах одного слоя, можно предположить, что действующие электростатические силы в пределах слоя не стабильны, в результате чего имеется вращательная мода, которая поворачивает каждый тетраэдр так, что два других тетраэдра в этой элементарной ячейке вращаются в противоположных направлениях. Структура должна стабилизироваться пространственным перераспределением заряда между ионом А и одним из атомов X тетраэдра. Потенциальная энергия внутри слоя может быть представлена двойной ямой: полиномом четвертой степени j. Взаимодействия между слоями проявляются в отталкивании между вершиной тетраэдра и основанием тетраэдра, лежащего в другом слое, а также через А ионы. Когда вдоль C-направления имеется два слоя на постоянную решетки (как например в Rb₂ZnBr₄), то потенциальная энергия взаимодействия ионов может быть охарактеризована вращением пирамиды в n-ом слое на угол φ_n   и представлена в форме аналогичной дискретной φ⁴ задачи в ANNNI модели [120]:

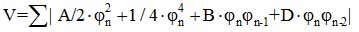   (4.2)

 

 Как известно,в этом случае   имеются   нелинейные   решения    (например "солитоны"). Для расчета параметров А, В и D необходимо знать всю специфику о межатомных взаимодействиях и структуру химической связи. Однако некоторые решения j⁴ модели имеют хаотический режим. Как показано [120,122], в частных случаях при небольших значениях ширины 1 "солитонов" относительно постоянной решетки (узкие солитоны), имеется несколько состояний высокого порядка соразмерности с небольшим расстоянием между солитонами l_о. При увеличении l_о   и достижении его величины некоторого критического значения l_cr, это смешанное состояние переходит в хаотическое поведение со случайно пиннингованными (анти)солитонами.

 Пытаясь удовлетворить данным нейтроновского, рентгеновского рассеяния и данным радиоспектроскопии, мы можем представить структуру несоразмерной фазы бесконечным набором фрагментов с длинным периодом, которые отличаются между собой неэквивалентностью химической связи в субфрагментах, расположенных в структурной ячейке определенным образом. Например, если считать что в N₄ фазе Rb₂ZnBr₄ ячейка кристалла имеет размер 14 постоянных решетки, то она может иметь подструктуру составленную из двух фрагментов с длиной в 3а_о и двух в 4а_о постоянных решетки расположенных относительно друг друга случайным образом (смешанные нелинейные решения). В примитивном описании ограничиваясь четырнадцатью тетраэдрами (в их двухминимумном либрационном положении), мы можем составить субячейку 3а_о, например, из одного тетраэдра в левом и двух в правом положении, а субячейку 4а_о из двух левых и двух правых последовательно расположенных тетраэдров. Тогда ячейка 14а_о может быть представлена пятью способами (основные решения) последовательного положения двух подЪячеек 3а_о и двух подячеек 4а_о. Один из этих способов может оказаться более благоприятным. В более полном смысле структура определяется конкретным общим нелинейным решением.

Распространяя такое построение структуры на высокотемпературную область Rb₂ZnBr₄, можно пытаться описать переход структуры 5/17 к 1/3 или 1/4 для каждого атома галогена тетраэдра через небольшое перераспределение электронной плотности в группе соседних атомов (вспышки поляризации). При осуществлении одного такого процесса размер ячейки уменьшается через серию ступеней до 3а_о или 4а_о. Модуляция представляется не непрерывным смещением ядер от положения к положению, а перераспределением электронной плотности двух упорядоченных энергетически близких структур 3а_о   и 4а_о.

Согласно этим представлениям, по данным ЯКР в Rb₂ZnBr₄ под давлением в широкой температурной области от T_i до 230⁰K вблизи атмосферного давления наблюдается режим смешанного длиннопериодического и хаотического поведения. Это видно из сравнения наблюдаемой формы спектра, которая непосредственно после отжига представлена размытыми частотными распределениями. В этом случае дифракционные данные, где наблюдается размытый сателлит в одном положении (≈5/17), видят только периодичность структуры. В области Т_c перехода в F фазу длиннопериодическое поведение превалирует над хаотическим. А при повышении давления к фазе H, хаотическое поведение почти полностью исчезает и "сатанинская лестница" проявляется более четко (complete). При этом фаза 2/7 является по структуре зависящей от предистории комбинацией фаз ≈1/3 и ≈1/4. Фазы N есть смесь длиннопериодических фаз с небольшой примесью хаотических. При повышении давления в области J_C и М фаз, число энергетически эквивалентных наборов длиннопериодических и хаотических фаз, согласно [13], может увеличиваться. Линии фазовых переходов в этом случае представляют области, где осуществляется смена среднего волнового вектора. Мы можем предположить, что при фазовом переходе M₁↔M₂ происходит изменение волнового вектора q_S хаотической структуры 1/4 к 1/5 или 1/6 через промежуточное значение типа q_S ≈0.222 ≈ 1/4-d . Поэтому методами дифракции здесь возможно наблюдение еще одной узкой фазы, как предсказывается моделью Обри [12] и было зарегистрировано в (NH₄)₂ZnCl₄ [47,50] и (NH₄)₂ZnBr₄ , (Рис.1.6).

 Форма резонансной линии в области несоразмерной фазы может отражать определенный тип смешанного между состояниями q_δ≈l/4 и q_δ≈l/3 нелинейного решения.

 Таким образом, сравнение теоретических фазовых диаграмм, с Р-Т диаграммой из данных ЯКР и с учетом данных нейтроновского рассеяния, позволяет сделать предположение, что с увеличением давления в RZB должны наблюдаться структуры типа 1/5, 1/6, 1/8 и т.д., с приближением к точке Лифшица. Что касается изменения структуры в области модулированной фазы, то можно предположить существенное наличие в Rb₂ZnBr₄ взаимодействий, расстраивающих пространственную кристаллическую симметрию. Основу для описания преобразования структуры и эволюции спектров ЯКР, с этой точки зрения, следует искать в осуществлении конкуренции электрического взаимодействия между подрешетками структуры и ее связью с фононным спектром. Наличие пространственной нелинейной поляризации в соединениях данного класса давно установлено. Она обусловлена значительным искажением и поворотом групп ВX₄ и неоднородной поляризацией электронов рыхлого остова атома В. В связи с этим возникают существенные электрические дипольные моменты атомных групп, величины которых отличаются для каждой группы как по величине, так и по направлению. Учет такого рода пространственно-неоднородных нелинейных электрических вкладов может существенным образом изменить подход в описании формы резонансных спектров в соединениях семейства А₂ВX₄. Причину неоднородности необходимо искать в тонкостях природы химической связи.

И наконец, мы можем также провести сравнение теоретической фазовой диаграммы Обри с экспериментальными данными по изменению величины волнового вектора q_δ в других соединениях А₂ВX₄ (Табл.4.1).

С точки зрения кристаллохимии, относительные величины радиуса катиона А соединения А₂ВX₄ можно условно разделить на две группы. В первой группе, с крупным катионом Cs, наблюдается следующая последовательность преобразования структур:

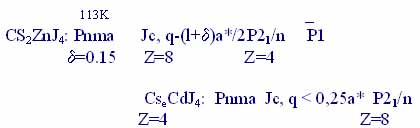
   В Cs₂CdJ₄,   Cs₂CdBr₄   последовательности   преобразования структур и величина q_δ в Ic близки к таковым для Cs₂CdJ₄. Во второй группе, со средним и малым радиусом катиона, наблюдается иная последовательность преобразования структуры, характеризующаяся низкотемпературной фазой с пространственной группой Pn2₁a, но с разной кратностью объема элементарной ячейки относительно высокотемпературной. Так для Rb₂ZnBr₄ под давлением имеем

 

  

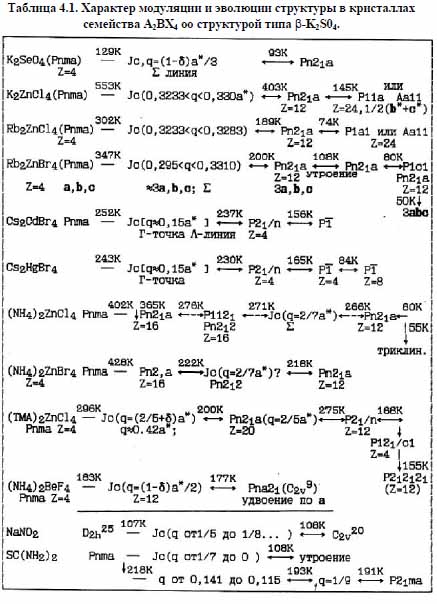
Таблица 4.1. Характер модуляции и эволюции структуры в кристаллах семейства А₂ВХ₄ оо структурой типа b-K₂S0₄.

 

 

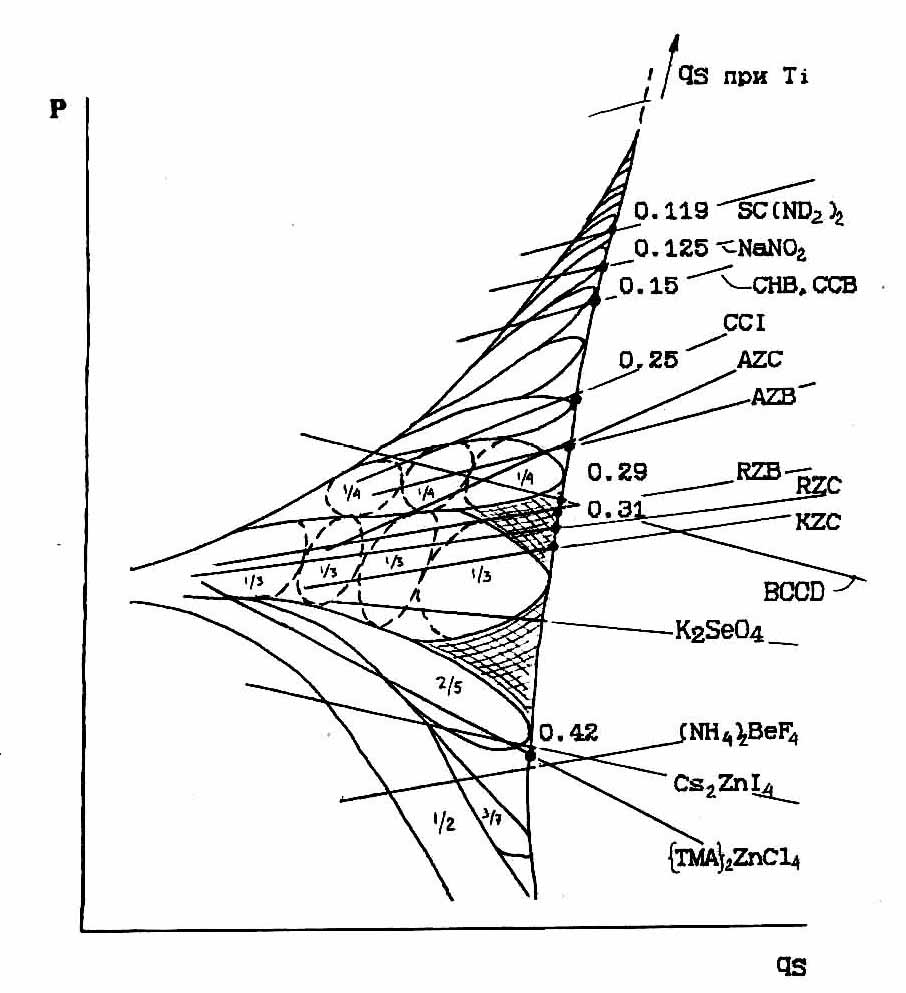
Рис.40.   Сравнение экспериментальных данных изменения волнового вектора  q_δ в разных соединеиях типа β-K₂SO₄ с теоретической фазовой диаграммой [12].

 

Основные результаты работы

 1. Для прецизионных ЯКР исследований фазовых переходов созданы безградиентные термоприставки и камера высокого давления, обладающие оптимальным согласованием с приемной частью стандартного спектрометра квадрупольного резонанса.

 2. Исследована последовательность фазовых переходов в Cs₂CdJ₄. Впервые методом ЯКР обнаружена несоразмерная фаза в b модификации этого кристалла. Взаимно дополняющими экспериментальными способами построена схема изменения симметрии. Методом рентгеноструктурного анализа подтверждено наличие несоразмерной фазы.

 3. Изучена последовательность фазовых переходов в кристалле Cs₂ZnJ₄. Методом ЯКР ¹²⁷J зарегистрирована несоразмерная фаза, обнаружена широкая   температурная   область   предпереходного упорядочения.   Сделано предположение и подтверждено изменение симметрии при фазовых переходах в этом соединении.

 4. Автором синтезировано и исследовано методом ЯКР соединение (NH₄)₂ZnJ₄. По переходу 1/2 ↔ 3/2 ¹²⁷J обнаружено три фазовых перехода. Форма линий и особенности температурного поведения частот позволяют утверждать, что промежуточные фазы в кристалле (NH₄)₂ZnJ₄ являются несоразмерными.

 5. Проведены температурные измерения времен Тq₁ и T_Q2 спиновой релаксации ядер ¹²⁷J.   Установлено существенное влияние спин-спиновой релаксации ядер галогена на корректность регистрации формы резонансной линии в несоразмерной фазе. Зафиксирован двухмасштабный характер ядерной динамики в Cs₂ZnJ₄.

 6. Обнаружены полиморфные модификации кристалла Rb₂ZnBr₄ и Cs₂CdJ₄. - a↔b. Установлено, что b-модификация в соединениях   Cs₂CdJ₄ и Rb₂ZnBr₄ является метастабильной. Выяснены условия осуществления a↔b перехода.

7. Методом ЯКР построена и исследована фазовая Р-Т диаграмма Rb₂ZnBr₄ в области несоразмерной фазы до давлений более 1.0ГПа. Обнаружены последовательности высокосимметричных и несоразмерно разупорядоченных фаз высокого давления. Интерпретация экспериментальных данных ЯКР в рамках "дьявольской лестницы" не противоречит дифракционным измерениям и теоретическим псевдоспиновым-ANNNI моделям несоразмерных фаз. 

 

Заключение

Проведенные в   работе   исследования демонстрируют возможности импульсного метода ЯКР при изучении разупорядаченных структур, в том числе при высоком гидростатическом давлении.

На базе разработанной аппаратуры для проведения температурных и высокого давления измерений исследованы последовательности фазовых переходов в ряде соединений с несоразмеренными фазами.

На основе полученных данных о степени динамического и структурного упорядочения ядер в исследованных соединениях может быть разработана модель преобразования атомной структуры.

Автор признателен научному руководителю кандидату физико-математических наук А. К. Москалеву за помощь в работе над рукописью и полезные советы. Благодарит фонд Сороса за финансовую поддержку.

 

Диссертация    автореферат    оглавление    §1.1   §1.2.   §1.3   §1.4   §2.1   §2.2-4   §3.1-2   §3.3-4   §4.1   § 4.2.   § 4.3   §4.4   заключение   ссылки 

  pdf:   Глава 1     Глава 2     Глава 3    Глава 4    Библиография     Диссертация вся pdf     English      pdf