§ 1.2 Радиоспектроскопические методы исследования несоразмерно-модулированных структур.
Радиоспектроскопические методы исследования веществ основаны на возбуждении переходов между энергетическими уровнями системы ядерных спинов посредством радиочастотного поля. В случае твердых кристаллических тел взаимодействие радиополя с ядерными или электронными спинами, находящимися в кристаллическом поле атомов представляется в виде:
H = Hо + H1+….. (1.6)
где Hо - гамильтониан взаимодействия спина с электронно-ядерным окружением атомов кристалла, H1 - взаимодействие о РЧ-полем.
В общем виде, в связи с обычной симметричностью ядерных волновых функций, гамильтониан кристаллического поля атомов Hо можно представить через разложение в ряд по четным степеням спиновых моментов [19,24]:
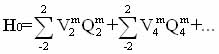(1.7)
где Qi - операторы связанные с проекцией спиновых операторов; Vim, - коэффициенты, выражающиеся через параметры внутри и межатомных взаимодействий. Симметрия этих коэффициентов, в частности, зависит от симметрии кристаллической решетки и при фазовом переходе в основном определяется симметрией мягкой моды.
В случае ядерного квадрупольного резонанса (ЯКР) рассматривается взаимодействие сферически несимметричного ядра атома с неоднородным электрическим полем электронов окружения. Кулоновская энергия этого взаимодействия имеет вид [25]:
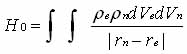(1.8)
где rе и rn - плотности электронных и ядерных зарядов; rn-rе - расстояние между взаимодействующими объемами зарядов dVе и dVn. Пользуясь разложением
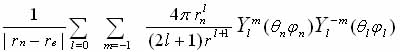(1.9)
по сферическим и радиальным функциям и вводя обозначения Vi для l-го члена разложения потенциала от электронов дипольных моментов ядра
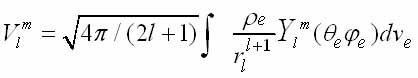(1.10)
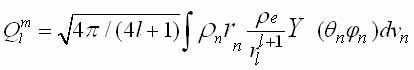
и переходя к операторам, получим гамильтониан взаимодействия ядерного электрического момента с атомными электронами в виде (1.7). Ядерное квадрупольное взаимодействие описывается членом
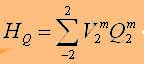(1.11)
где, как хорошо известно [24], операторы Q2m выражаются через операторы спина ядра I, Iz, I-, I+ ,а компоненты оператора V2m через компонты тензора ГЭП qαβ:
(1.12)
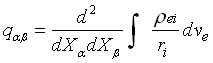
В простейшем приближении рассматривается модель точечных зарядов, колеблющихся вблизи узлов ri кристаллической решетки.
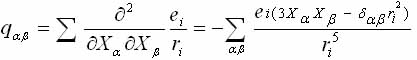(1.13)
Возвращаясь к выражению (1.7), мы видим, что коэффициенты V2m,4 определяются, в частности характером атомных смещений в кристалле и в общем случае могут быть представлены через статическую и динамическую части этих смещений [19,27]:
(1.14)
в высокосимметричной фазе большинство из V2m,4 равны нулю. В искаженной фазе один (или более) из коэффициентов становится oтличным от нуля и может быть разложен по степеням параметра порядка Q=u
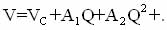(1.15)
С учетом флуктуации Q, выше Ti:
(1.16)
Для тензора ГЭП это разложение в более подробной записи с формальным переобозначением символов представляется в виде [19,27]: при Т > Ti
<Vij>=Vij(0)+SAk2<Qc(k,t)>+... (1.17)
при Т > Ti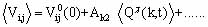 
где Q(qs-k,t)= áQ(qs-k,t )ñ + dQ(qs-k,t ) - статическая и флуктуационная части параметра порядка вблизи точки конденсации мягкой моды qs. Спектральная функция критической переменной Q(k,t) имеет вид [19]:
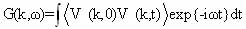(1.18)
и согласно разложению Vij(k,t) может быть представлена в виде
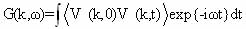(1.19)
где V(k,O)V(k,t) разделен на статическую и временную части. Если временно-зависящая часть v(k,t) является медленной функцией времени, то для волнового вектора qs компонента спектральной функции отклика
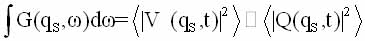(l.20)
с учетом вкладов по к вблизи qs, форма линии будет иметь вид (с учетом первого члена разложения):
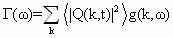(1.21)
таким образом форма линии отражает форму функции распределения искажений атомной конфигурации, вызванную движением, медленным в масштабе времени радиосигнала. Ширина линии характеризует при этом величину вкладов в среднеквадратичное искажение, обусловленных фурье-компонентами поля смещений с частотами, малыми по сравнению с обратной величиной временного порога разрешения радиосигнала ( 1/Т*2Q). Если в низкотемпературной фазе наблюдается какое-либо преимущественное колебание около положений,смещенных на некоторую величину ±Q0(T) от высокосимметричного положения, то линия будет состоять из двух компонент. При T→Ti Q0→0 и расщепление становится малым по сравнению с (медленными) флуктуациями предпереходного упорядочения. В атом случае линия спектра сужается до минимума при достижении верхней границы переходного упорядочения. Когда линейые по Q члены, сравнимы по величине с квадратичными, то необходимо учитывать также вклад рамановских процессов релаксации в ширину линии. Наконец, необходимо отметить, что форма линии Г(ω ) определяется всеми волновыми векторами к фононов. В связи о этим, для анализа результатов необходимо иметь какое-либо модельное представление для g(k, ω).
Выражение (1.17) для преобразования тензора ГЭП вблизи фазового перехода указывает, что из радиоспектроскопических исследований возможно извлечение информации о поведении параметра порядка Q(Qs-k,t). Так уже при Т > Ti измерения <Q(t)> дают возможность оценить временно усредненный квадрат критической координаты, которая в предпереходной области связана с критической динамикой. В частности, это относится к кристаллам, где фазовый переход связывается с увеличением амплитуды флуктуации, обусловленных решеточными колебаниями или либрационными модами. Временно-зависящая часть ГЭП определяется скоростью и типом процессов, с которой спин-решеточная система может обмениваться энергией. Поэтому, как следует из (1.17), возможно изучать микроскопическую динамику критических колебаний, то есть величину изменения флуктуации параметра порядка вблизи Ti .
С точки зрения радиоспектроскопии вопрос заключается в том, как корректно возбудить спиновую систему и измерить скорость спин-решеточной релаксации, разделить различные вклады и затем связать измеренные величины с динамикой критического колебания. В случае ЯКР возбуждении ядерной системы осуществляется переменным магнитным полем H1. Гамильтониан, описывающий радиочастотное воздействие на систему ядерных спинов, в случае непрерывного зондирования имеет вид:
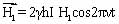(1.22)
где n - частота РЧ поля, γ - гиромагнитное отношение.
Вероятность перехода в единицу времени между состояниями cк и c1 в этом случае определяется выражением [30, 135]:
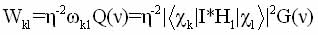(1.23)
Wk1- относительные вероятности переходов, G(ν)- функция спектрального распределения резонансной линии. Интенсивность поглощения в условиях резонансного возбуждения зависит от разности населенности уровней, и, при отсутствии насыщения, определяется выражением [26, 29]:
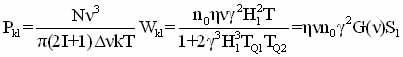(1.24)
N- число ядер, Δν - полуширина линии поглощения.
При импульсном возбуждении спиновой системы квантовомеханические операторы зависят от времени и для вычисления амплитуды переходных сигналов обычно используется метод матрицы плотности [30]. В этом случае изменение статического оператора плотности s описывается уравнением Неймана:
.. (1.25)
H0(t)- оператор квадрупольного взаимодействия, H1(t)- оператор взаимодействия с РЧ полем H1 cosnt. Последний оператор равен нулю между импульсами. Решение уравнения (1.25) представляется в виде [31,135] s = R-1σ0R, где R=RIRtRIIRt+t. RI и RII - решения уравнения Шрёдингера в период действия импульсов (интервалы нутации); Rt и Rt +t - для интервалов свободной прецессии между импульсами.
Разработанные методы решения уравнения (1.25) позволяют рассчитать амплитуду сигналов индукции Aτ, Aτ+t и спинового эхо Aτ+t при двухимпульсном возбуждении ядер со спином 3/2 [32]. Огибающая спинового эхо, как показано, может быть представлена в виде двух слагаемых - члена пропорционального величине постоянной составляющей и члена соответствующего сигналу индукции, который мал если T*Q2 < τ < TQ2 (TQ2↔T*Q2). Исследования спектральных функций переходных сигналов нам не известны. Однако, при соблюдении определенных спектральных условий, и в частных случаях, обращаясь к непосредственному сравнению, есть основания для выбора таких условий импульсного возбуждения, когда спектральная форма резонансного отклика будет сопоставима с формой возбуждаемой непрерывным зондированием.
Обратимся к описанию известной феменологической модели статических и динамических характеристик несоразмеренных фаз [33,34]. В адиабатическом приближении форма резонансной линии описывается выражением [27]
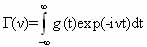где 
(1.26)
что в статическом переделе выглядит как
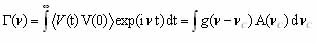(1.27)
Если считать, что при фазовом переходе, частота резонансного поглощения ядер может быть разложена в ряд по степеням смещений
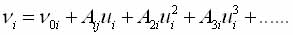(1.28)
где ui может быть представлена в виде разложения по собственным векторам мягкой моды (1.1), то для каждого атома сорта р можно написать(нелокальное описание) [35]:
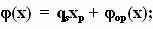(1.29)
где в приближении плосковолновой модуляции (ПВМ) фаза атомных смещений изменяется как:
φ(х) = qsxp + φop(х); (1.30)
и в солитонном приближении:
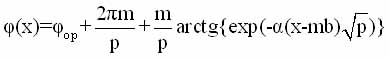(1.31)
Если модуляция длинно-периодическая, то после подстановки (29) в (28) получим ~
n(X)= no + n1cos(y(x)+j) + n'2 + n2сos2y(x)+ ... (1.32)
Плотность спектральной функции f(ν) согласно [33] будет определяться выражением:
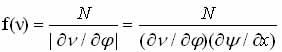(1.33)
гдe N - число ядер на единице длины в направлении вектора несоразмерной модуляции. В случае длиннопериодической модуляции f(ν) представляет сумму частотных дискретных компонент от каждого узлa элементарной ячейки.
Конкретный вид разложения определяется локальной и кристаллической симметрией узла решетки для которого производится разложение, а именно, симметрией электронного окружения и симметрией собственных векторов мягкой моды. Это накладывает ограничения на вид разложения (1.28), и некоторые из коэффициентов Aki могут быть равны нулю (A1¹0, A2=0 - линейное разложение, A1=0, A2¹0 - квадратичное разложение и т.д.).
Анализ функции f(ν) был выполнен для всевозможных случаев разложения ν(x). Первые результаты были получены в предположении, что резонансная частота νo1 рабочего ядра зависит только от синфазно смещающихся с ним атомов (локальное описание) [34]. Для иллюстрации на Рис.1.3 представлен вид функций f(ν) и температурное расщепление краевых сингулярностей относительно положения высокосимметричной фазы для квадратичного случая в ПВМ приближении.
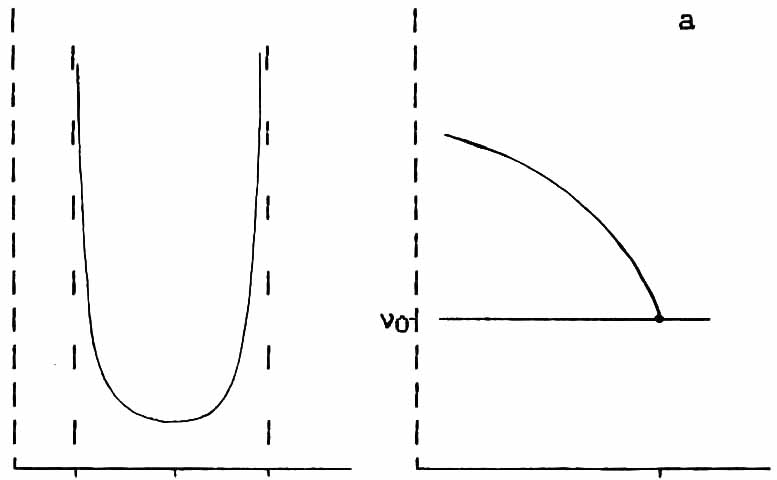
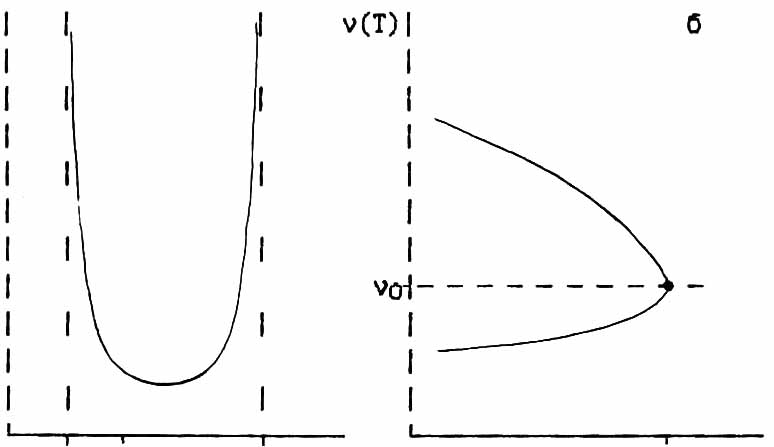
Рис.1.З. Вид функции f(ν) и расцепление частот при Ti в а) локальном и б) нелокальном случаях.
В дальнейшем, было феменологически учтено влияние на ГЭП даннного ядра смещения атомов близлежащего окружения, связанных с другими собственными векторами мягкой моды (нелокальное описание) [35]. В этом случае удалось достичь большего согласия с экспериментом. С теоретической точки зрения анализировались и вопросы спин-решеточной релаксации ядер в несоразмеренных системах [33,35].
Таким образом имеется теоретическая основа для описания резонансных спектров в неооразмеренных системах, как в статическом, так и в динамическом аспектах. Задачей экспериментальных исследований является получение данных для сопоставления.
Диссертация автореферат оглавление §1.1 §1.2. §1.3 §1.4 §2.1 §2.2-4 §3.1-2 §3.3-4 §4.1 § 4.2. § 4.3 §4.4 заключение ссылки
pdf: Глава 1 Глава 2 Глава 3 Глава 4 Библиография Диссертация вся pdf English pdf